(解题报告)

前言

A,B水题，E,I原题
实际赛时400分（乐多毁我青春）

C 大水题

题目

如果有一个长度为\(n\)的数组\(a[1],a[2],\cdots,a[n]\)，对于非负整数\(k\)，若令\(b[i]=a[i] \oplus k\)，满足bb是一个单调不下降的数组，即满足\(b[1]\le b[2]\le \cdots \le b[n]\)，则称\(k\)是数组\(a\)的完美数，其中\(\oplus\)表示按位异或。

现在给出一个长度为\(n\)的数组\(a\)，并进行\(q\)次修改，每次会改变\(a\)中的一个数。要求在第一次修改前以及每一次修改后求出当前数组的最小完美数，若不存在则输出\(-1\)。

分析

从局部到整体考虑，如果相邻两个数\(x,y\)，改变这两个数大小关系当且仅当一个二进制位是0一个是1的最高位被改变，那么可以用两个数组表示某个位置是否必然改变或必然不改变，累加次数，它待修改就先减掉再加上修改后的情况，如果两个数组的某一位都大于0，那么必然输出\(-1\),接着只要必然修改的位置数组大于0，那么就必须要让这一位变成1，时间复杂度\(O(30(n+q))\)

代码

#include <cstdio>
#include <cctype>
#define rr register
using namespace std;
int n,a[1000011],ac[31],wa[31];
inline signed iut(){
    rr int ans=0; rr char c=getchar();
    while (!isdigit(c)) c=getchar();
    while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
    return ans;
}
inline signed get_top(int x){
    for (rr int i=30;~i;--i)
        if ((x>>i)&1) return i;
    return -1;
}
inline void Add(int x){
    rr int t=get_top(a[x]^a[x+1]);
    if (t==-1) return;
    if (a[x]<=a[x+1]) ++ac[t]; else ++wa[t];
}
inline void Del(int x){
    rr int t=get_top(a[x]^a[x+1]);
    if (t==-1) return;
    if (a[x]<=a[x+1]) --ac[t]; else --wa[t];
}
inline bool check(){
    for (rr int i=30;~i;--i)
    if (ac[i]&&wa[i]) return 0;
    return 1;
}
inline void print(int ans){
    if (ans>9) print(ans/10);
    putchar(ans%10+48);
}
inline void doit(){
    if (check()){
        rr int sum=0;
        for (rr int i=30;~i;--i)
        if (wa[i]) sum|=1<<i;
        print(sum);
    }else putchar('-'),putchar(49);
}
signed main(){
    n=iut();
    for (rr int i=1;i<=n;++i) a[i]=iut();
    for (rr int i=1;i<n;++i) Add(i);
    doit();
    for (rr int Q=iut();Q;--Q){
        rr int x=iut(),y=iut();
        if (x>1) Del(x-1);
        if (x<n) Del(x);
        a[x]=y;
        if (x>1) Add(x-1);
        if (x<n) Add(x);
        putchar(10); doit();
    }
    return 0;
}

D 简单数据结构题

题目

对于一个长度为\(n\)的序列\(a_1,a_2,\cdots,a_n\)，找一个整数\(k\)使得\(\max\limits_{1\le i\le n}(a_i\oplus k)\)尽可能小，其中\(\oplus\)表示按位异或。

样例输入：3 1 2 3 样例输出：2

分析

首先数据结构要确定，选择\(\text{Trie}\),接着建好一个 \(\text{Trie}\)，样例如图所示（简化版）

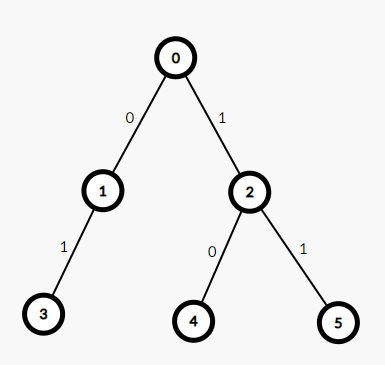
首先这棵树整棵树肯定得用，所以要搜索，如果遇到一个分支怎么办，如果不把这一位变成1，答案肯定会变大，但是这一位变成1，我把它给大的答案肯定得不偿失，所以把小的那一条路这一位变成1，继续跳到上一行

代码

#include <cstdio>
#include <cctype>
#include <queue>
#define rr register
using namespace std;
const int N=100001;
int trie[N<<5][2],tot,n,a[N],ans=1<<30;
inline signed iut(){
    rr int ans=0; rr char c=getchar();
    while (!isdigit(c)) c=getchar();
    while (isdigit(c)) ans=(ans<<3)+(ans<<1)+(c^48),c=getchar();
    return ans; 
}
inline signed min(int a,int b){return a<b?a:b;}
inline void Insert(int x){
    rr int p=0;
    for (rr int i=29;~i;--i){
        rr int t=(x>>i)&1;
        if (!trie[p][t]) trie[p][t]=++tot;
        p=trie[p][t];
    }
}
inline signed dfs(int p,int now){
    if (!trie[p][0]&&!trie[p][1]) return 0;
    rr int t,cnt=0;
    if (trie[p][0]) t=dfs(trie[p][0],now-1),++cnt;
    if (trie[p][1]) t=min(t,dfs(trie[p][1],now-1)),++cnt;
    if (cnt==2) t|=1<<now;
    return t;
}
signed main(){
    n=iut();
    for (rr int i=1;i<=n;++i) Insert(a[i]=iut());
    return !printf("%d",dfs(0,29));
}

G 简单01背包题

（题目名称过分）~(实际这个题目更过分)

题目

给你一堆物品，希望你做一个01背包，输出最大能获得的价值（容量和体积很大，但是价值为1、2）

分析

赛时数据太水，被部分背包水过，然而正解我也还没写

未完待续

SSL新年欢乐赛暨BPM退役赛

原文：https://www.cnblogs.com/Spare-No-Effort/p/12207684.html