对于整数\(n\)的阶乘,我们有\(n!=n\times (n-1)...\times1\)。
对于实数\(x\)的阶乘,计算公式为:
\[
\Gamma(x)=\int_0^\infty t^{x-1}e^{-t}\,dt
\]
性质如下:
将Gamma函数标准化可以得到:
\[
\int_0^\infty \frac{t^{\alpha-1}e^{-t}}{\Gamma(\alpha)}\,dt = 1
\]
这就是简单的Gamma分布:
\[
Gamma(t|\alpha)=\frac{t^{\alpha-1}e^{-t}}{\Gamma(\alpha)}
\]
此时做\(t=\beta x\):
\[
\int_0^\infty \frac{(\beta x)^{\alpha-1}e^{-\beta x}}{\Gamma(\alpha)}\,d(\beta x) = 1
\]
就可以得到Gamma分布的一般形式:
\[
Gamma(t|\alpha,\beta)=\frac{\beta^\alpha x^{\alpha-1}e^{-\beta x}}{\Gamma(\alpha)}
\]
其中\(\alpha\)为形状参数(shape parameter),决定了分布曲线的形状;\(\beta\)为逆尺度参数(inverse scale parameter),决定曲线有多陡。
当\(\alpha = k+1,\ \ \beta = 1\)时:
\[
Gamma(x)=\frac{x^ke^{-x}}{\Gamma(k+1)}=\frac{x^ke^{-x}}{k!}
\]
这正是泊松分布的分布函数。由此看来Gamma分布是泊松分布在实数域上的扩展。
在贝叶斯理论中,后验分布如下计算:
\[
g(\theta|x)=\frac{g(\theta)f(x;\theta)}{f(x)}=c_xL(\theta,x)g(\theta)
\]
\(f(x)\)表示观察样本的边缘密度(marginal density),是只关于变量\(x\)的概率分布,不考虑其他变量。\(f(x;\theta)=L(\theta,x)\)是似然函数(样本的分布)(likelihood or sampling distribution),\(g(\theta)\)是其先验分布。
其中:
\[
c_x^{-1}=f(x)\f(x)=\int f(x;\theta)g(\theta)\,d\theta
\]
此公式解释了边缘密度,可以理解为\(\theta\)取某一值时,我们得到观察值样本的概率的积分。
当\(g(\theta)\)与\(g(\theta|x)\)的形式相同时,我们说这是共轭分布,\(g(\theta)\)为共轭先验。(没有共轭后验的说法)
为何使用共轭先验?
可以使得先验分布和后验分布的形式相同,这样一方面合符人的直观(它们应该是相同形式的)另外一方面是可以形成一个先验链,即现在的后验分布可以作为下一次计算的先验分布,如果形式相同,就可以形成一个链条。
为什么没有共扼后验?
如果先验分布和似然函数可以使得先验分布和后验分布(posterior distributions)有相同的形式,那么就称先验分布与似然函数是共轭的。所以,共轭是指的先验分布(prior probability distribution)和似然函数(likelihood function)。如果某个随机变量Θ的后验概率 p(θ|x)和气先验概率p(θ)属于同一个分布簇的,那么称p(θ|x)和p(θ)为共轭分布,同时,也称p(θ)为似然函数p(x|θ)的共轭先验。
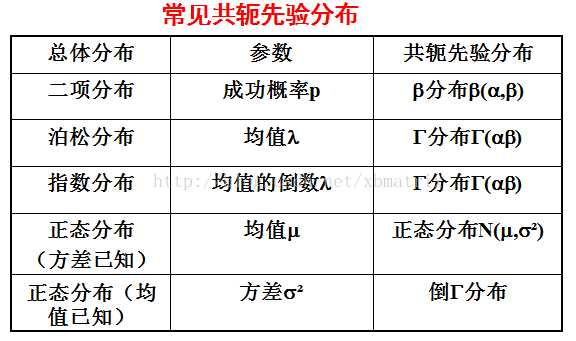
可以看到二项分布的共轭先验分布为Beta分布。
原文:https://www.cnblogs.com/LvBaiYang/p/12207630.html