树上问题总结

1.树上倍增求LCA

求LCA的方法1：tarjan
求LCA的方法2：倍增
求LCA的方法3：树链剖分

用树链剖分求LCA

#include<bits/stdc++.h>
using namespace std;

const int maxn = 5e5+100;
vector<int> g[maxn];
/*  父亲,    深度,       子节点数, 重儿子,   dfs序,   dfs映射，链头,    链尾    */
int fa[maxn],depth[maxn],sz[maxn],son[maxn],id[maxn],rk[maxn],top[maxn],bot[maxn];
int cnt = 0;

void dfs(int x,int deep){
    depth[x] = deep;
    sz[x] = 1;
    for(int li = 0;li<g[x].size();li++){
        int i = g[x][li];
        if(i == fa[x]) continue;
        fa[i] = x;
        dfs(i,deep+1);
        sz[x] += sz[i];
        if(sz[i] > sz[son[x]]) son[x] = i;
    }
}

void dfs2(int x,int tp){
    top[x] = tp;
    id[x] = ++cnt;
    rk[cnt] = x;
    if(son[x]) dfs2(son[x],tp),bot[x] = bot[son[x]];
    else bot[x] = x;
    for(int li=0;li<g[x].size();li++){
        int i = g[x][li];
        if(i != fa[x] && i != son[x])
            dfs2(i,i);
    }
}

int lca(int u,int v){
    while(top[u] != top[v]){
        if(depth[top[u]] < depth[top[v]]) swap(u,v);
        u = fa[top[u]];
    }
    if(depth[u] < depth[v]) return u;
    return v;
}

int main(){
    ios::sync_with_stdio(false);
    int n,m,root;
    cin>>n>>m>>root;
    for(int i=1;i<=n-1;i++){
        int u,v;
        cin>>u>>v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    dfs(root,1);
    dfs2(root,root);
    while(m--){
        int u,v;
        cin>>u>>v;
        cout<<lca(u,v)<<endl;
    }
    return 0;
}

2.树上前缀和

例题1: 前缀和+lca

题目描述：给定一颗n个点的树，每个点i的点权为vi；q个询问，求点u，到点v路径上的点权和。1<=n,q<=10^5;0<=vi<=10^9

设点u和v的lca为点x，点x的父亲为点y；
点u到点v的路径ans = sum[v] + sum[u] - sum[x] - sum[y];
注释：减去lca，减去lca的父亲，lca以上的路径被减了两遍。

3-0.树上差分概念

利用树上倍增求出两点的LCALCA，然后两点(u,v)(u,v)之间边的信息往往可以转化为(u?>root)+(v?>root)?2?(LCA?>root)，点的信息可以转化为(u?>root)+(v?>root)?LCA?>root?faLCA?>root。

3-1.树上差分，对点差分

例题1如下：

差分后，每个点的现在值等于原值+子树中所有变化之和。

设点u和v的lca为点x，点x的父亲为点y；
a[u] += t; a[v] += t; a[x] -= t; a[y] -= t;

例题2：HPU校赛，树上异或路径和

3-2.树上差分，对边差分

对边差分的公式：(u?>root)+(v?>root)?2?(LCA?>root)

例题1：P2420
这道题 异或两次(LCA->root) = 不异或

例题2：树上前缀和 + 异或 + 组合数学



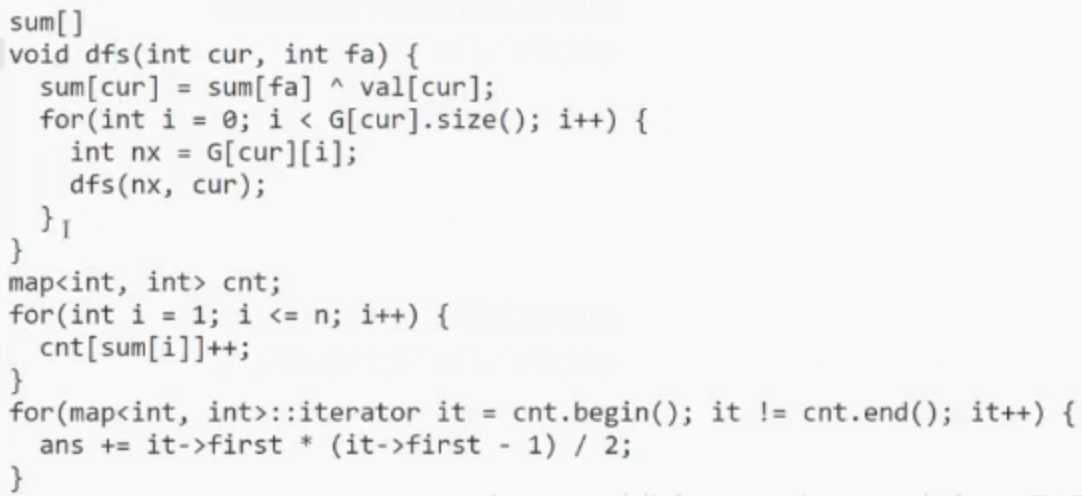
first改成second

4.子树问题：dfs序

dfs序把树上问题转成区间序列问题，之后用线段树主席树等数据结构处理序列问题即可

例题：

5.树链问题：树链剖分

树链剖分把树上问题，把各个链(重链、轻链）转成连续的区间序列，之后用线段树主席树等数据结构处理序列问题即可；

模板题：
P3384题目
p3384题解
用树链剖分实现4种树上问题：

1.将树从x到y结点最短路径上所有节点的值都加上z
2.求树从x到y结点最短路径上所有节点的值之和
3.将以x为根节点的子树内所有节点值都加上z
4.求以x为根节点的子树内所有节点值之和

例题6：

例题7：

树上问题

原文：https://www.cnblogs.com/fisherss/p/12213531.html