prufer序列

• 定义

Prufer数列是无根树的一种数列。在组合数学中，Prufer数列由有一个对于顶点标过号的树转化来的数列，点数为n的树转化来的Prufer数列长度为n-2。

• 描述

eg

1. 将Prufer数列转化成树的方法

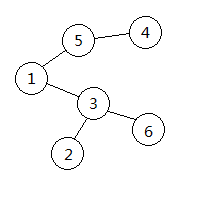
　　一种生成Prufer序列的方法是迭代删点，直到原图仅剩两个点。对于一棵顶点已经经过编号的树T，顶点的编号为{1,2,...,n}，在第i步时，移去所有叶子节点（度为1的顶点）中标号最小的顶点和相连的边，并把与它相邻的点的编号加入Prufer序列中，重复以上步骤直到原图仅剩2个顶点。

对于例子有：

　　首先在所有叶子节点中编号最小的点是2，和它相邻的点的编号是3，将3加入序列并删除编号为2的点。接下来删除的点是4，5被加入序列，然后删除5，1被加入序列，1被删除，3被加入序列，此时原图仅剩两个点（即3和6），Prufer序列构建完成，为{3,5,1,3}

1. 将Prufer数列转化成树的方法

　　设{a1,a2,..an-2}为一棵有n个节点的树的Prufer序列，另建一个集合G含有元素{1..n}，找出集合中最小的未在Prufer序列中出现过的数，将该点与Prufer序列中首项连一条边，并将该点和Prufer序列首项删除，重复操作n-2次，将集合中剩余的两个点之间连边即可。

对于例子有：

　　Prufer序列为{3,5,1,3}，开始时G={1,2,3,4,5,6}，未出现的编号最小的点是2，将2和3连边，并删去Prufer序列首项和G中的2。接下来连的边为{4,5},{1,5},{1,3},此时集合G中仅剩3和6，在3和6之间连边，原树恢复。

（参考自度娘）

• 性质

1. prufer序列中某个编号出现的次数就等于这个编号的节点在无根树中的度数-1
2. 一棵n个节点的无根树唯一地对应了一个长度为n-2的数列，数列中的每个数都在1到n的范围内。
3. n个点的无向完全图的生成树的计数：n^(n−2)，即n个点的有标号无根树的计数
4. n个节点的度依次为d1,d2,…,dn的无根树共有(n−2)!/∏n i=1(di−1)!个，因为此时Prufer编码中的数字i恰好出现di−1次，(n−2)!是总排列数
5. n个点的 有标号有根树的计数：n^(n−2) ∗n=n^(n−1)

[HNOI2008]明明的烦恼（luogu）

• Description

题目描述

自从明明学了树的结构,就对奇怪的树产生了兴趣...... 给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树?

输入格式

第一行为N(0<N<=1000),接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1

输出格式

一个整数,表示不同的满足要求的树的个数,无解输出0

• Solution

数学推导（不会打式子）+质因数分解+高精乘法计算最后结果

• Code

#include <cstdio>
#include <cstdlib>
#define ll long long
using namespace std;
const int N=1010,base=10000;
ll a[N];
int n,k,d[N],sum,ans[N];
void add(int x,ll c)
{
    for(int i=2;i<=x;i++)
        while(x%i==0) x/=i,a[i]+=c;
}
void re()
{
    puts("0");
    exit(0);
}
void print()
{
    printf("%d",ans[ans[0]]);
    for(int i=ans[0]-1;i>0;i--)
        printf("%04d",ans[i]);
    printf("\n");
}
void mul(ll x)
{
    for(int i=1;i<=ans[0];i++) ans[i]*=x;
    for(int i=1;i<=ans[0];i++)
        ans[i+1]+=ans[i]/base,ans[i]%=base;
    while(ans[ans[0]+1])
        ans[0]++,ans[ans[0]+1]+=ans[ans[0]]/base,ans[ans[0]]%=base;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&d[i]);
        if(d[i]==0) re();
        if(d[i]!=-1) k++,sum+=d[i]-1;
    }
    if(sum>n-2) re();
    for(int i=n-2;i>n-2-sum;i--) add(i,1);
    for(int i=1;i<=n;i++)
        for(int j=2;j<d[i];j++)
            add(j,-1);
    add(n-k,n-2-sum);
    ans[0]=ans[1]=1;
    for(int i=2;i<=n;i++)
        for(int j=1;j<=a[i];j++) mul(i);
    print();
    return 0;
}

[HNOI2008]明明的烦恼（prufer序列，高精度，质因数分解）

原文：https://www.cnblogs.com/hsez-cyx/p/12221097.html