转载请标明出处,以下部分内容部分引自Ivanovcraft 巨佬的博客,加上了一些自己的见解和自己的代码。
对于修改树上的点权值,我们可以想到用树上差分来做。
对于求两点之间路径上的点的权值和,我们可以利用倍增的思想很好的解决这个问题。
可是,当修改与查询结合起来,就不能把这两种方法简单结合起来了。(这样的话复杂度会很劣)
于是乎,就要引出我们今天的主角了———树链剖分
树链剖分,计算机术语,指一种对树进行划分的算法,它先通过轻重边剖分将树分为多条链,保证每个点属于且只属于一条链,然后再通过数据结构(树状数组、BST、SPLAY、线段树等)来维护每一条链。(来自百度百科)
让我们先来认识几个概念:
重儿子:父亲节点的儿子中子树最大(节点数最多)的儿子;
轻儿子:父亲节点的儿子中除重儿子以外的其他儿子;
重边:连接父节点和重儿子的边;
轻边:连接父节点和亲儿子的边;
重链:由一条或多条重边连接形成的路径;
轻链:由一条或多条轻边连接形成的路径。
P.S.:若父节点中存在多个节点数最多的儿子,就随便取其中一个作为它的重儿子。
认识完这些概念,再让我们看看树链剖分的原理吧!
先放一张图片(以下图片来自百度百科)
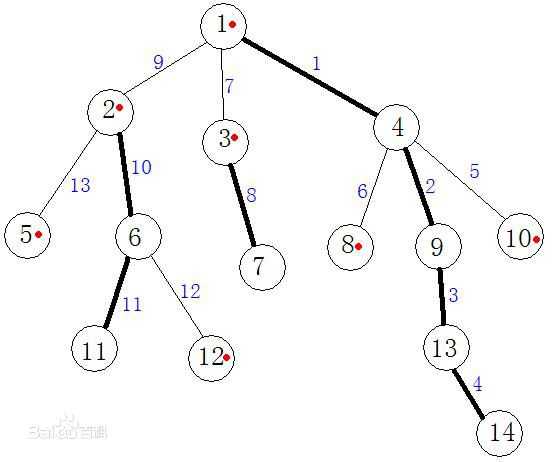
呐,这就是一个树链剖分的标准图了。图中标粗的都是重边,其余的边都是轻边。
其中,用红点标记的是指该节点是当前节点所在重链的顶端。
对于每个节点所在重链的顶端,我们用一个top数组来记录。
对于修改和查询,我认为其核心在于通过跳重链使两个节点跳到一条重链上,然后再进行计算。
我们可以先dfs一遍记录每个节点的父节点(fa数组)和子树大小(sz数组),然后计算出除叶节点外的节点的重儿子(son数组)。
以下是代码:
1 void dfs1(int po,int step) 2 { 3 dep[po]=step;sz[po]=1; 4 for(int i=hd[po];i;i=e[i].n) 5 { 6 int v=e[i].v; 7 if(v!=fa[po]) 8 { 9 fa[v]=po; 10 dfs1(v,step+1); 11 sz[po]+=sz[v]; 12 if(sz[v]>sz[son[po]]) son[po]=v; 13 } 14 } 15 }
然后我们需再dfs一遍,使得一棵子树内的节点编号连续,一条重链上的编号连续(先遍历重儿子,然后再遍历轻儿子),这样我们就可以利用线段树等数据结构来将树上的信息转化为线性信息来处理了。
以下是代码:
1 void dfs2(int po,int tp)//tp为当前重链的顶端 2 { 3 top[po]=tp;rk[po]=++tot;id[tot]=po; 4 if(son[po]) dfs2(son[po],tp);//先遍历重儿子的子树 5 for(int i=hd[po];i;i=e[i].n) 6 { 7 int v=e[i].v; 8 if(v!=fa[po]&&v!=son[po]) dfs2(v,v);//轻儿子的重链顶端即为它自己 9 } 10 }
这里需要注意的是,我们用rk数组来记录当前节点对应线段树上的区间(其实也是dfs序(先遍历重儿子的子树)),然后用id数组进行对应。
对于一棵子树中的修改查询,由于一棵子树内的编号连续,在线段树上一个节点对应的子树编号即为[rk[x],rk[x]+sz[x]-1]。
然后我们就可以很快乐地用线段树来进行区间信息维护了~~
对于两点之间路径的点的修改查询,就与上有一点点不同了。其实通过手动模拟可以看出,当两个点的所在的重链不同时,由两个节点中重链顶端节点的深度较大者先往上跳到重链顶端,通过线段树修改/查询由该节点到重链顶端的路径上的节点信息,再跳到轻边到重链顶端的父亲,一直循环,直到两个节点跳到同一条重链上,然后直接查询/修改目前两点路径中的信息就可以了。
修改代码如下:
1 void add1(int u,int v,int addv) 2 { 3 int fu=top[u],fv=top[v]; 4 while(fu!=fv) 5 { 6 if(dep[fu]<dep[fv]) swap(u,v),swap(fu,fv); 7 add2(rt,1,n,rk[fu],rk[u],addv); 8 u=fa[fu],fu=top[u]; 9 } 10 if(dep[u]<dep[v]) swap(u,v); 11 add2(rt,1,n,rk[v],rk[u],addv); 12 }
查询代码如下:
1 ll query1(int u,int v) 2 { 3 ll res=0; 4 int fu=top[u],fv=top[v]; 5 while(fu!=fv) 6 { 7 if(dep[fu]<dep[fv]) swap(u,v),swap(fu,fv); 8 (res+=query2(rt,1,n,rk[fu],rk[u]))%=P; 9 u=fa[fu],fu=top[u]; 10 } 11 if(dep[u]<dep[v]) swap(u,v); 12 (res+=query2(rt,1,n,rk[v],rk[u]))%=P; 13 return res; 14 }
其中add2、query2都是在线段树上的操作。
提供代码:

1 #include <iostream> 2 #include <cstdio> 3 #define gc cl==cr&&(cr=(cl=bu)+fread(bu,1,100000,stdin),cl==cr)?EOF:*cl++ 4 #define gs (ch<‘0‘||ch>‘9‘) 5 #define r(x) x=read() 6 #define ls po<<1 7 #define rs po<<1|1 8 using namespace std; 9 typedef long long ll; 10 const int N=1e5+111; 11 int n,m,R,P,tot,rt; 12 char bu[100011],*cr,*cl; 13 int read() 14 { 15 int x=0,f=1;char ch=gc; 16 while(gs) {if(ch==‘-‘) f=-1;ch=gc;} 17 while(!gs) x=x*10+ch-48,ch=gc; 18 return x*f; 19 } 20 int v[N],hd[N],dep[N],fa[N],sz[N],son[N],top[N],id[N],rk[N]; 21 struct edge{ 22 int n,v; 23 }e[N<<1]; 24 void add(int u,int v) 25 { 26 e[++tot]=(edge){hd[u],v}; 27 hd[u]=tot; 28 } 29 void dfs1(int po,int step) 30 { 31 dep[po]=step;sz[po]=1; 32 for(int i=hd[po];i;i=e[i].n) 33 { 34 int v=e[i].v; 35 if(v!=fa[po]) 36 { 37 fa[v]=po; 38 dfs1(v,step+1); 39 sz[po]+=sz[v]; 40 if(sz[v]>sz[son[po]]) son[po]=v; 41 } 42 } 43 } 44 void dfs2(int po,int tp) 45 { 46 top[po]=tp;rk[po]=++tot;id[tot]=po; 47 if(son[po]) dfs2(son[po],tp); 48 for(int i=hd[po];i;i=e[i].n) 49 { 50 int v=e[i].v; 51 if(v!=fa[po]&&v!=son[po]) dfs2(v,v); 52 } 53 } 54 struct node{ 55 ll sum,addv; 56 int l,r; 57 }tr[N<<2]; 58 59 void update(int po) {(tr[po].sum=tr[ls].sum+tr[rs].sum)%=P;} 60 61 void build(int po,int l,int r) 62 { 63 tr[po].l=l,tr[po].r=r; 64 if(l==r) 65 { 66 tr[po].sum=v[id[l]]%P; 67 return; 68 } 69 int mid=l+r>>1; 70 build(ls,l,mid);build(rs,mid+1,r); 71 update(po); 72 } 73 void down(int po) 74 { 75 (tr[ls].sum+=tr[po].addv*(tr[ls].r-tr[ls].l+1)%P)%=P; 76 (tr[ls].addv+=tr[po].addv)%=P; 77 (tr[rs].sum+=tr[po].addv*(tr[rs].r-tr[rs].l+1)%P)%=P; 78 (tr[rs].addv+=tr[po].addv)%=P; 79 tr[po].addv=0; 80 } 81 void add2(int po,int l,int r,int ql,int qr,int addv) 82 { 83 if(ql<=l&&qr>=r) 84 { 85 (tr[po].sum+=addv*(tr[po].r-tr[po].l+1))%=P; 86 (tr[po].addv+=addv)%=P; 87 return; 88 } 89 if(tr[po].addv) down(po); 90 int mid=l+r>>1; 91 if(mid<qr) add2(rs,mid+1,r,ql,qr,addv); 92 if(ql<=mid) add2(ls,l,mid,ql,qr,addv); 93 update(po); 94 } 95 void add1(int u,int v,int addv) 96 { 97 int fu=top[u],fv=top[v]; 98 while(fu!=fv) 99 { 100 if(dep[fu]<dep[fv]) swap(u,v),swap(fu,fv); 101 add2(rt,1,n,rk[fu],rk[u],addv); 102 u=fa[fu],fu=top[u]; 103 } 104 if(dep[u]<dep[v]) swap(u,v); 105 add2(rt,1,n,rk[v],rk[u],addv); 106 } 107 int query2(int po,int l,int r,int ql,int qr) 108 { 109 if(ql<=l&&r<=qr) return tr[po].sum%P; 110 if(tr[po].addv) down(po); 111 int mid=l+r>>1; 112 if(mid<ql) return query2(rs,mid+1,r,ql,qr); 113 else if(mid>=qr) return query2(ls,l,mid,ql,qr); 114 else return (query2(ls,l,mid,ql,mid)+query2(rs,mid+1,r,mid+1,qr))%P; 115 update(po); 116 } 117 ll query1(int u,int v) 118 { 119 ll res=0; 120 int fu=top[u],fv=top[v]; 121 while(fu!=fv) 122 { 123 if(dep[fu]<dep[fv]) swap(u,v),swap(fu,fv); 124 (res+=query2(rt,1,n,rk[fu],rk[u]))%=P; 125 u=fa[fu],fu=top[u]; 126 } 127 if(dep[u]<dep[v]) swap(u,v); 128 (res+=query2(rt,1,n,rk[v],rk[u]))%=P; 129 return res; 130 } 131 int main() 132 { 133 r(n),r(m),r(R),r(P); 134 for(int i=1;i<=n;i++) r(v[i]); 135 for(int i=1;i< n;i++) 136 { 137 int u,v; 138 r(u),r(v); 139 add(u,v);add(v,u); 140 } 141 tot=0;dfs1(R,1); 142 dfs2(R,R); 143 build(rt=1,1,n); 144 for(int i=1;i<=m;i++) 145 { 146 int f,x,y,z; 147 r(f); 148 switch(f) 149 { 150 case 1:r(x),r(y),r(z);add1(x,y,z);break; 151 case 2:r(x),r(y);printf("%lld\n",query1(x,y));break; 152 case 3:r(x),r(y);add2(1,1,n,rk[x],rk[x]+sz[x]-1,y);break; 153 case 4:r(x);printf("%lld\n",query2(1,1,n,rk[x],rk[x]+sz[x]-1));break; 154 } 155 } 156 return 0; 157 }
感谢大家的阅读~这是本人第一次写这种类型的博客(学习笔记),如有不足,大家可以提出来哦~
再次感谢Ivanovcraft 巨佬的博客。
原文:https://www.cnblogs.com/P-Y-Y/p/12229977.html