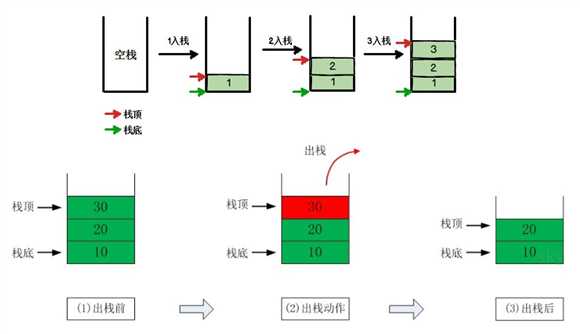
计算器
子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出,以回到原来的程序中
处理递归调用:和子程序的调用类似,只是除了储存下一个指令的地址外,也将参数、区域变量等数据存入堆栈中
表达式的转换:[中缀表达式→后缀表达式] 与 求值(实际解决)
二叉树的遍历
图形的深度优先(depth一first)搜索法
/**
* 使用 [数组] 来模拟栈
* 入栈:stack[++top] = data;
* 出栈:value = stack[top--];
*/
public class ArrayStack {
private int maxSize;
private int[] stack;
private int top = -1;
public ArrayStack(int maxSize) {
super();
this.maxSize = maxSize;
stack = new int[this.maxSize];
}
// 栈满
public boolean isFull() {
return top == maxSize-1;
}
// 空栈
public boolean isEmpty() {
return top == -1;
}
// 入栈
public void push(int value) {
// 判断栈是否满
if(isFull()) {
System.out.println("栈满");
return;
}
stack[++top] = value;
}
// 出栈
public int pop() {
// 判断栈是否空
if(isEmpty())
throw new RuntimeException("空栈");
return stack[top--];
}
// 遍历栈 (栈顶→栈底)
public void showStack() {
if(isEmpty()) {
System.out.println("栈空, 没有数据");
return;
}
for(int i = top; i >= 0; i--)
System.out.printf("stack[%d] = %d", i, stack[i]);
}
}
public class LinkedListStack {
private int maxSize;
private Node head;
private Node top;
public LinkedListStack(int maxSize) {
super();
this.maxSize = maxSize;
head = new Node();
top = head;
}
// 栈满
public boolean isFull() {
int count = 0;
Node temp = head.next;
while(temp != null) {
count++;
temp = temp.next;
}
return count == maxSize;
}
// 空栈
public boolean isEmpty() {
return top == head;
}
// 入栈
public void push(int val) {
if(isFull()) {
System.out.println("栈满");
return;
}
Node n = new Node();
n.data = val;
top.next = n;
top = n;
}
// 出栈
public int pop() {
if(isEmpty())
throw new RuntimeException("空栈");
Node temp = head;
while(temp.next != top)
temp = temp.next;
int val = top.data;
top = temp;
return val;
}
// 遍历栈
public void showStack() {
if(isEmpty()) {
System.out.println("栈空, 没有数据");
return;
}
Node reHead = new Node();
Node cur = head.next;
Node next;
while(cur != null) {
next = cur.next;
cur.next = reHead.next;
reHead.next = cur;
cur = next;
}
cur = reHead.next;
while(cur != null) {
System.out.println(cur);
cur = cur.next;
}
}
}
class Node {
public int data;
public Node next;
@Override
public String toString() {
return "Node [data=" + data + "]";
}
}

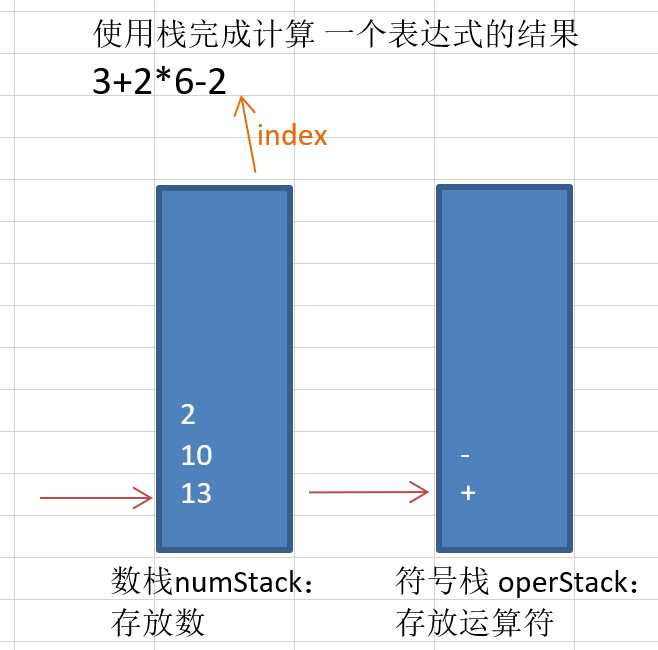
public class Calculator {
public static void main(String[] args) {
// 算式
String expression = "17*2*2-123+1-5+3-4";
char[] expressionArr = expression.toCharArray();
// 创建 [数栈] 和 [符号栈]
CalcStack numStack = new CalcStack(10);
CalcStack operStack = new CalcStack(10);
// 定义相关变量
// -- 用于扫描的索引
int index = 0;
// -- 用于拼接多位数字构成的数据
String keepNum = "";
int num1, num2, oper, result;
// -- 将每次扫描得到的char保存到此
char ch = ' ';
// 扫描表达式
while(index != expressionArr.length) {
// 依次得到每一个字符
ch = expressionArr[index];
if(operStack.isOper(ch)) { // ch 是符号
// ∵ 是符号 ∴ 要判断 当前符号栈是否为空
if(!operStack.isEmpty()) {
if(operStack.priority(ch) <= operStack.priority(operStack.peekTop())) {
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
result = numStack.cal(num1, num2, oper);
// 运算结果入 [数栈]
numStack.push(result);
// 当前操作符 入 [符号栈]
operStack.push(ch);
} else { // 当前操作符的优先级 > 栈顶的操作符的优先级
operStack.push(ch);
}
} else {
operStack.push(ch);
}
} else { // ch 是数字
/*
* numStack.push(ch); X
* ∵ 在ASCII码表中, '1' —— 49 ∴这么写是错误的
* numStack.push(ch - 48); X
* ∵ 无法处理单个数据是多位数的情况, 如 24, 123
* ∴ 当处理数字时, 不能直接入栈, 应判断该数据是否还有余下的位数
* 1. 定义一个字符串变量, 用于拼接数字
* 2. 得到首位数字后, 追加进字符串
* 3. 向index指向位置之后再看一眼
* 3.1 是数字, 再次追加
* 3.2 是符号, 则将字符串入栈, 注意清空字符串以便下次使用
*/
keepNum += ch;
// 如果ch已经是算式的末位, 就直接入栈
if(index == expressionArr.length-1)
numStack.push(Integer.parseInt(keepNum));
else {
if(operStack.isOper(expressionArr[index+1])) {
numStack.push(Integer.parseInt(keepNum));
// 记得清空!!!
keepNum = "";
}
}
}
index++;
}
// 从 [数栈] 和 [符号栈] 中 pop 出相应的 数据 和 符号,进行运算
// 若符号栈为空, 则数栈中肯定只剩一个数字, 其就是算式结果
while(!operStack.isEmpty()) {
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
result = numStack.cal(num1, num2, oper);
numStack.push(result);
}
System.out.printf("%s = %d", expression, numStack.peekTop());
}
}
class CalcStack {
private int maxSize;
private int[] stack;
private int top = -1;
public CalcStack(int maxSize) {
super();
this.maxSize = maxSize;
stack = new int[this.maxSize];
}
// 栈满
public boolean isFull() {
return top == maxSize-1;
}
// 空栈
public boolean isEmpty() {
return top == -1;
}
// 入栈
public void push(int value) {
// 判断栈是否满
if(isFull()) {
System.out.println("栈满");
return;
}
stack[++top] = value;
}
// 出栈
public int pop() {
// 判断栈是否空
if(isEmpty())
throw new RuntimeException("空栈");
return stack[top--];
}
public int peekTop() {
return stack[top];
}
// 遍历栈 (栈顶→栈底)
public void showStack() {
if(isEmpty()) {
System.out.println("栈空, 没有数据");
return;
}
for(int i = top; i >= 0; i--)
System.out.printf("stack[%d] = %d", i, stack[i]);
}
// 返回运算符优先级(拟定为:优先级使用数字表示, 数字越大, 则优先级越高)
public int priority(int oper) {
if(oper == '*' || oper == '/')
return 1;
else if(oper == '+' || oper == '-')
return 0;
else
return -1; // 目前算式只包含加减乘除
}
// 判断是否为一个运算符
public boolean isOper(char val) {
return val == '+' || val == '-' || val == '*' || val == '/';
}
// 计算
public int cal(int num1, int num2, int oper) {
int result = 0;
switch (oper) {
case '+':
result = num2 + num1;
break;
case '-':
result = num2 - num1;
break;
case '*':
result = num2 * num1;
break;
case '/':
result = num2 / num1;
break;
}
return result;
}
}
原文:https://www.cnblogs.com/liujiaqi1101/p/12231384.html