这学期同时上了计算机图形学和计算方法两门课,学到这部分的时候突然觉得de Casteljau递推算法特别像牛顿插值,尤其递推计算步骤很像牛顿差商表。
一开始用伯恩斯坦多项式计算Bezier曲线的时候,由于其多项式的计算十分不利于计算机实现,还会出现数值不稳定的情况
所以后来出现了de Casteljau算法,以下PPT截图来自北京化工大学李辉老师
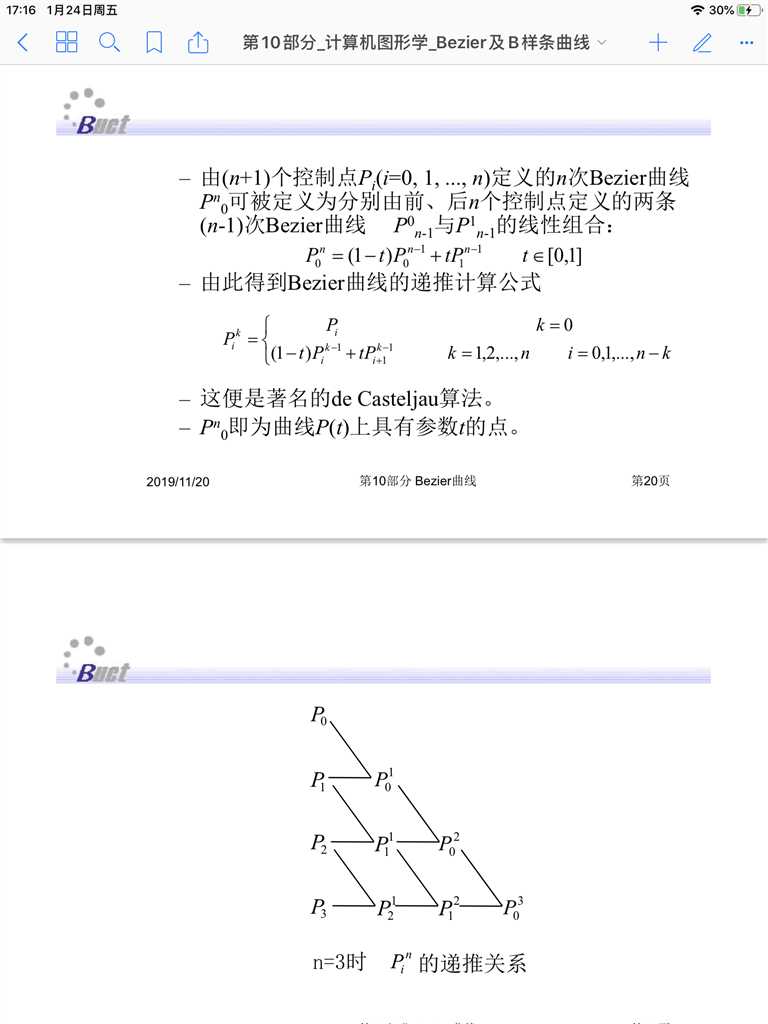
实现代码(六个顶点):
import numpy as np import matplotlib.pyplot as plt #B = (1-t)*P0+t*P1 def one_bezier_curve(a, b, t): return (1-t)*a + t*b #使用de Casteljau算法求解曲线 def n_bezier_curve(x, n, k, t): #当且仅当为一阶时,递归结束 if n == 1: return one_bezier_curve(x[k], x[k+1], t) else: return (1-t)*n_bezier_curve(x, n-1, k, t) + t*n_bezier_curve(x, n-1, k+1, t) def bezier_curve(x, y, num, b_x, b_y): #n表示阶数 n = len(x) - 1 t_step = 1.0 / (num - 1) t = np.arange(0.0, 1+t_step, t_step) for each in t: b_x.append(n_bezier_curve(x, n, 0, each)) b_y.append(n_bezier_curve(y, n, 0, each)) if __name__ == "__main__": x = [int(n) for n in input(‘x:‘).split()] y = [int(n) for n in input(‘y:‘).split()] plt.plot(x, y) # x = [0, 2, 5, 10, 15, 20] # y = [0, 6, 10, 0, 5, 5] num = 100 b_x = [] b_y = [] bezier_curve(x, y, num, b_x, b_y) plt.plot(b_x, b_y) plt.show()
运行截图:
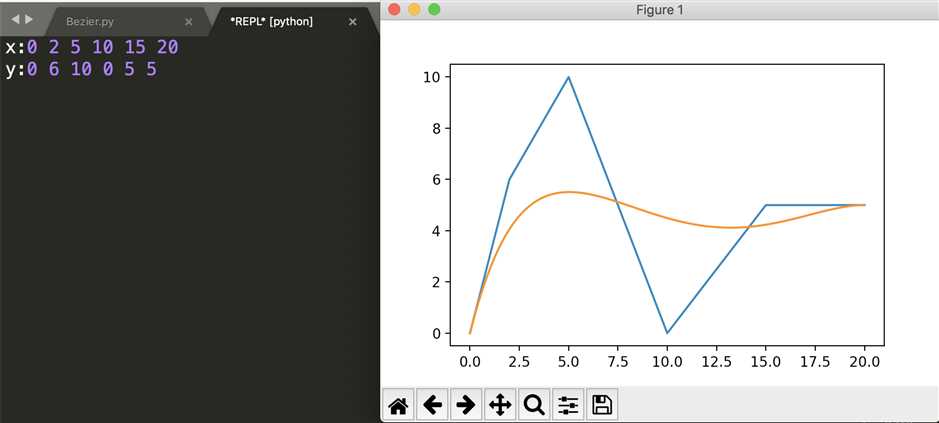
原文:https://www.cnblogs.com/swenw/p/12232391.html