简单,就是将输入判别为两种类别之一的问题。
例如,输入:一张彩色图片(RGB三个通道三个矩阵,unroll得到特征向量);输出:是或不是(1或0)猫
训练样本:\((x,y),x\in R^n, y\in \{0,1\}\)
包含m个样本的数据集:\( \{(x^{(1)}, y^{(1)}), \dots, (x^{(m)}, y^{(m)}) \}\)
为了方便,常用矩阵表示\( \boldsymbol{X} = (x^{(1)}, \dots, x^{(m)}) \),即每一列表示一个特征向量,我们也称\( \boldsymbol{X} \in R^{n \times m} \)为数据矩阵。
同理,\( \boldsymbol{Y} = (y^{(1)}, \dots, y^{(m)}), Y \in R^{1 \times m} \)
也没什么好讲的,给定输入的特征向量,希望得到其类别为1的概率,也就是 \( \hat{y}=P(y=1|x) \),实现这一目标的方法有很多,取决于我们选择的模型。在logistic回归中,我们采用的是 \( \hat{y}=\sigma (w^Tx+b), \sigma(z)=\frac{1}{1+e^{-z}} \)
这里吴恩达区分了损失函数(loss function)和代价函数(cost function)。
损失函数和误差函数(error function)相同,通常指单个样本,例如回归问题常用的均方误差:\( L(\hat{y}, y)=\frac{1}{2}(\hat{y}-y)^2 \),二分类问题常用的交叉熵:\( L(\hat{y}, y)=-y\ln\hat{y}-(1-y)\ln(1-\hat{y}) \);
代价函数通常指整个数据集:\( J(w,b)=\frac{1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)}, y^{(i)}) \)
选择交叉熵作为二分类问题的损失函数的好处在于待求解问题是一个凸优化问题,而使用均方误差则不能保证。
这节也非常简单,机器学习中大多数问题的求解最后都归结为一个优化问题,即求最值问题。有些优化问题有闭式解,如线性回归,而有些优化问题没有闭式解时,如logistic回归。解决方法就是用迭代优化算法,梯度下降法是最常用的迭代优化算法,是一阶近似。
某一点的梯度是一个矢量,其方向代表该点函数值增加最快的方向,而我们要解决的问题通常是一个最小化问题,那么只要沿着负梯度方向,按照合适的步长逐步前进就可以到达函数的极小值点(对于凸优化问题就是最小值点)。从前面的描述可以看出,梯度下降法的结果依赖于初始位置和步长。
这两节是吴恩达老师给同学补充微积分(其实只是简单的导数)知识的。跳过~
输入变量的复合运算可以表示成计算图,其中每一级运算表示成一个包含中间变量的节点,这样在梯度反向传播时可以更清晰直观地观察链式法则。
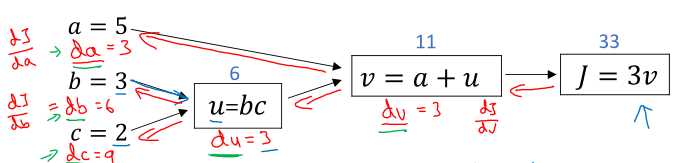
考虑到我们关注的总是最终输出对各个中间变量的导数,为了更简洁的表示(编程中也是),将\( \frac{dJ}{dv} \)记为\( dv \),其他的类似。
这节讲logistic回归中单个样本的梯度下降法,其实就是链式法则求梯度的一个例子,同样可以借助计算图进行计算。
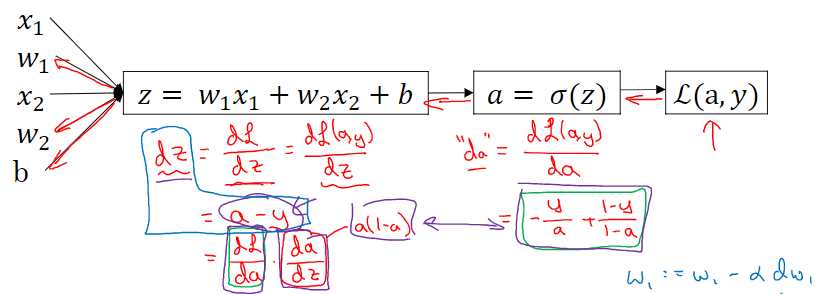
其中sigmoid函数的导数形式非常简单,配合交叉熵损失函数可以看到
\( \frac{dL(a,y)}{dz}=(-\frac{y}{a}+\frac{1-y}{1-a}) \times a(1-a)=a-y \)
这里的\( a \)其实就是\( \hat{y} \),这样就非常舒服了。
前面讲的是单个样本,对于整个训练集代价函数的梯度,就是将m个样本的梯度做累加平均。这样梯度下降法每更新一次就要遍历整个训练集,程序实现可以用向量化技巧来代替for循环。
尽可能的使用向量化计算(主要是矩阵乘法)代替显式for循环可以极大的提升计算速度,因为python中的numpy库等充分利用了CPU或GPU的并行化计算能力,而for循环做不到。如利用numpy库代替for循环进行各种运算:
相乘相加 → 矩阵乘法
for + math.exp() → np.exp()
还有np.abs(), np.log(), np.maximum(), v**2(ndarray类型)等等
将前面介绍的向量化技巧应用到logistic回归中,例如计算z:
\( Z=w^TX+[b, b, \dots, b]) \)
在python中只需要一个表达式:
Z = np.dot(w.T, X) + b
注意这里的b虽然只是一个实数,但在计算时python自动将其展成一个向量,这就是python的广播机制。
下面给出完整的logistic向量化实现:
Z = np.dot(w.T, X) + b A = sigmoid(Z) dZ = A - Y dw = np.dot(X, dZ.T) / m db = np.sum(dZ) / m w = w - a * dw b = b - a * db
其实numpy中可以用@表示np.dot()
注意这里的矩阵或者向量运算都是基于numpy的数组(ndarray)的。
广播机制简单的说就是当参与 +, -, *, / 运算的两个数组形状不一样时,python自动地将其中一个数组复制扩展成另外一个数组的形状,然后进行逐元素运算。当然这样做的前提是在它的能力范围之内,我总结了以下两点:
比如数组A的形状是(2,3,4),数组B的形状是(1,3,1),数组C的形状是(1,4),称A的型数为3,3个型的维数分别为2,3,4。因为A和B的型数相同,有一个型的维数相同且其它型的维数为1,所以可以直接进行A+B等操作;而A和C的型数虽然不同,但最后一个型的维数相同,所以也可以直接进行A+C等操作。
当然实际不要考虑那么复杂,我们常用的只是二维数组,如数组A形状(m,n),B形状(m,1),C形状(1,n),可以直接进行A+B,A+C等操作。
这节课中吴恩达老师在线编程,还是有一点问题的:
A = np.array([ [1,2,3,4], [5,6,7,8], ]) cal = A.sum(axis=0) per = 100 * A / cal.reshape(1,4)
其实在计算完sum之后,cal的形状应该是(4,),reshape之后才是(1,4),这两种结果虽然看起来差不多,但实际并不一样,比如(4,)不能进行转置。
从我个人的经验来看,最好将所有的向量都表示成二维数组,也就是1行n列或1列n行的矩阵,如(1,4),统一形式之后方便矩阵运算。但是在进行矩阵运算的过程中经常出现运算结果降维了,期望得到的是(1,4)的矩阵,却得到(4,)的数组,如果不加注意后面就可能出现bug。吴恩达老师教导我们,如果你算迷糊了,就多用reshape确保结果是你想要的形状,反正reshape的开销很小。
呃...尴尬,我前面提到的问题吴恩达在这一节做了专门讲解,很清楚,可怜我没有早看这个教程,吃了不少亏才总结出来。痛心!
老师的意思很清楚:
assert和reshape的开销都很小,这两点真的很实用,用起来!!
如果跟随Cousera课程的话需要用这个提交编程作业。Jupyter确实很好用,但我用不习惯嘿嘿,还是喜欢在VSCode里面写代码。
原文:https://www.cnblogs.com/tofengz/p/12228548.html