——based on tree-based cost aggregation & segment, 下称"ST"
answer: 建树思路不一样
answer:
本文目标是聚焦优化代价聚合(cost aggregation)模块的效果,主要分为:
局部法:通过设计窗口形状、大小以及滤波权重在窗口内实现局部最优代价聚合(窗口外的像素可看做权重为0),优点是速度快,缺点是结果为局部最优,通常使用一些具有"edge-aware"效应的局部滤波器直接对各视差层级进行滤波即可
全局法:通过构造能量函数或是建树,以全局代价值最小为目标来实现代价聚合,优点是精度高,缺点是速度慢
本篇文章主要是在NLCA的基础上继续基于树来优化,创新点是结合了分割和树来建树,建树过程中还可添加预定义的视差图来优化
ST和NL均是Minimum Spaning Tree(MST)在代价聚合模块的应用,MST在全局法的Dynamic Programming, graph cut, belief propagation中均有应用
实际上,STCA,NLCA都是另一种形式的滤波器设计,所以在Section future中,作者也有说将来会将本文思想拓展到edge-aware图像处理应用中
主要思想:
note: ST还支持输入视差图,利用此视差图 & RGB图像进行refine
贡献点:
时间性能:
| time | ST | ST-disp | MST | GF |
|---|---|---|---|---|
| total | 0.35s | 0.8s | 0.31s | 3.8s |
| build tree | 21ms | 34ms | 34ms | - |
关键文献:
【4】 P. F. Felzenszwalb and D. P. Huttenlocher. Efficient graph-based image segmentation. IJCV, 59(2):167–181, 2004.
【23】Q. Yang. A non-local cost aggregation method for stereo matching. In CVPR, pages 1402–1409, 2012.
——也是对比文献: 文中简称MST
【14】C. Rhemann, A. Hosni, M. Bleyer, C. Rother, and M. Gelautz. Fast cost-volume filtering for visual correspondence and beyond. In CVPR, pages 3017–3024, 2011.
——另一篇对比文献:文中简称GF

NLCA:
代价聚合本质:
\[C_d^A(p) = \sum_q{S(p, q)C_d(q)}\tag{1}\]
建树:
边:颜色相似度:
\[S(p, q)=S(q, p)=\exp(-\frac{D(p,q)}{\sigma})\tag{2}\]
节点:像素点
节点基于边的连接:参见基于kruskals构建最小生成树的思想:
https://www.cnblogs.com/biyeymyhjob/archive/2012/07/30/2615542.html
节点与节点间的联系:
遍历连接好的节点,记录节点间的连接关系(父节点,子节点,边权重的记录)
遍历:from leaf to root
滤波:
——树深度层次的代价传播
\[C_d^{A\uparrow}(v)=C_d(v) + \sum_{P(v_c)=v}{S(v, v_c)·C_d^{A\uparrow}(v_c)}\tag{3}\]
遍历:from root to leaf
——树广度层次的代价传播
\[C_d^A(v)=C_d^{A\uparrow}(v) + S(P(v), v)·\left[ C_d^A(P(v)) - S(v, P(v))· C_d^{A\uparrow}(v) \right] \\ = S(P(v), v)·C_d^A(P(v)) + \left[ 1 - S^2(v, P(v))\right]· C_d^{A\uparrow}(v) \tag{4}\]

从上图可以看出,STCA和NLCA做代价聚合的思路是一致的,深究每个模块算法发现,两者差异主要在于Build tree部分,下面着重记录下这部分
还是先来张流程图:
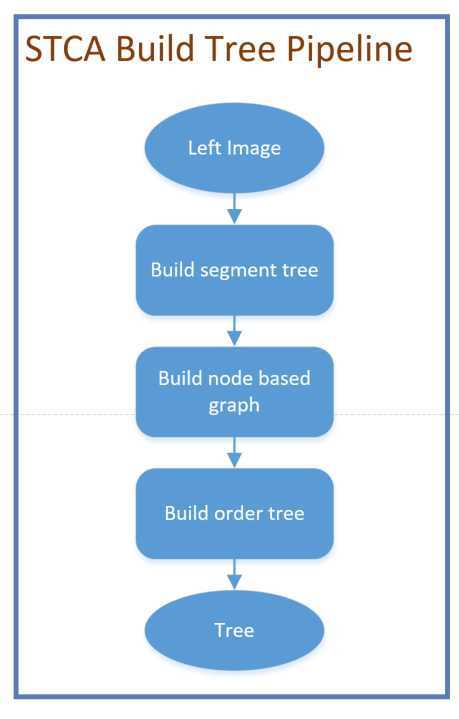
画完流程图,自己也发现没啥干货,再来一张作者的算法伪代码会清晰一些:

从前面作者介绍研究背景的时候可知,他们在建树的时候引入了图割的思想,也就是伪代码中讲的eg(6):
\[w_{ej} \le \min(Int(T_p) + \frac{k}{|T_p|}, Int(T_q)+ \frac{k}{|T_q|})\tag{6}\]
其中,\(Int(T_p)\)表示\(T_p\)中的最大边权重, \(k\)为常数,实验中设置为\(k=1200\)
除此之外,再补一个并查集的概念:
https://www.cnblogs.com/cyjb/p/UnionFindSets.html
零零散散铺垫了一些东西,还是借用作者的"Initialization -> Grouping -> Linking"以及上面的流程图来记录下建树的过程吧
build segment tree
Initialization
step 1: 以像素点为节点,相邻像素点之间的颜色相似度作为graph的edges权重;
在代码实现中,通过构建一个edge型数组来放置整张图的边和节点;
使用edge结构体来放置一条边的权重w,这条边连接的两个节点a和b;
为提升遍历速度和内存性能,只计算了当前点和右上角点之间的关系,并遍历每一个像素点。
Step 2: 对edge数组进行排序,这儿直接使用的std::sort,具体性能阔以和NLCA中杨庆雄取巧的排序手段做对比,这一步也对应着伪代码中的第1步。
Step 3: 作者自己定义了并查集的类universe,按照伪代码第2步进行初始化。
Grouping
Step 4: 对应着伪代码中的第6-12步,按照kruscal构造最小生成树的规则,从最小权重边开始遍历,判断其连接的两个点之间是否满足e.g.(6)的规则(e.g.(6)由文献[4]中所推导得到),如果满足,则把这两个点合为一个集合;
Linking
Step 5: 对应着伪代码中的第14-21步,就是将每个分割块连起来,最终得到一颗完整的树
从伪代码来看,到这一步,整个建树就完成了,实际上,为了更好的进行代价聚合,需要把新建立的树的父子节点关系记录下来;
build node based graph
这一步就是创建一个TreeNode数组把整棵树的父子节点关系建立起来,记录下他们之间的权重关系;
build order tree
这一步是一个类似家庭普查的过程,遍历所有边,统计每个节点的父亲节点索引,和他的权重关系,每个节点有多少儿子节点,并和每个儿子节点建立对应关系,记录和他的权重关系,注意,和上一步不同,这一步过后整棵树就是有序的了,便于后面的"from nodes to root"和"from root to nodes"的代价聚合;
滤波部分,同NLCA,先从叶子节点遍历到根节点,再从根节点遍历到叶子节点,理论就是前面介绍的公式(3)(4), 严格按照公式实现即可。
——在计算边权重的时候添加视差图信息来建树做优化,公式如下:
\[w_e = \lambda\frac{|I(s) - I(r)|}{\Delta_I} + (1 - \lambda) \frac{|D(s) - D(r)|}{\Delta_D}\tag{7}\]
一看公式便知,这里便不再赘述。
【论文笔记】Segment-Tree based Cost Aggregation for Stereo Matching
原文:https://www.cnblogs.com/nico-1729/p/12234022.html