查找:
在一些数据元素中,通过一定的方法找出与给定关键字相同的数据元素的过程
列表查找(线性表查找):
从列表中查找指定的元素
输入:列表、待查找元素
输出:元素下标(未找到元素的时候一般返回None或者-1)
顺序查找(Linear_Search):
def Linear_search(li, val):
for index, v in enumerate(li):
if v == val:
return index
else:
return
n为列表长度,没有循环迭代的过程
时间复杂度:
O(n)
二分查找(Binary_Search):
又叫折半查找,从有序列表的初始候选区li[0:n]开始,通过对待查找的值与候选区中间值的比较,可以使候选区减少一半
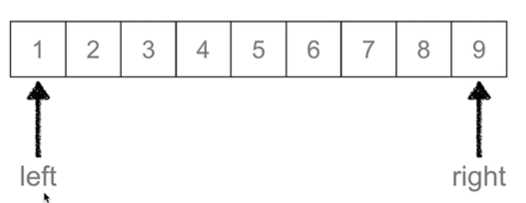
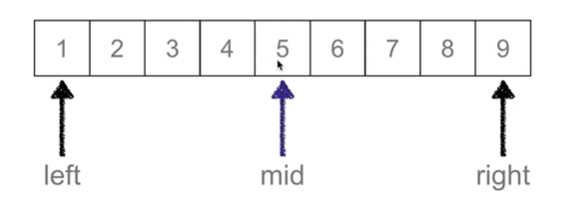
right = mid - 1
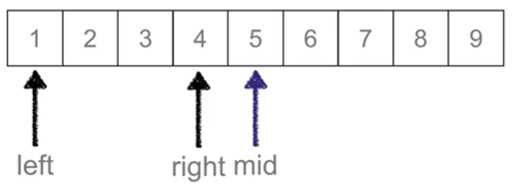
新的mid 就是2
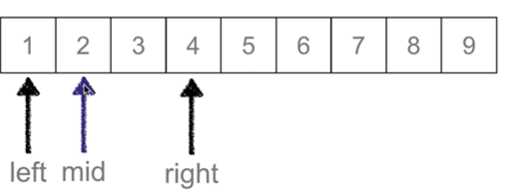
left = mid + 1
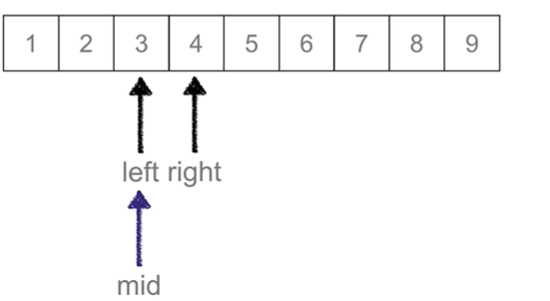
def Binary_Search(li, val):
left = 0
right = len(li)-1
while left <= right: # 候选区还有数值
mid = (left + right) // 2
if li[mid] == val:
return mid
elif li[mid] > val: # 查找的值在mid左侧
right = mid - 1
else: # li[mid] < val 说明带查找的值在mid的右侧
left = mid + 1
else:
return None
时间复杂度为 O(logn)
排序:

Bubble Sort (冒泡排序)
列表每两个相邻的数,如果前面比后面大,那么交换这两个数。
一趟排序完成后,则无序区减少一个数,有序区增加一个数。(出现最大的数)(n-1趟)
代码关键: 趟、无序区
时间复杂度 : O(n^2)
def bubble_sort(li):
for i in range(len(li) - 1): # 第i趟
exchange = False
for j in range(len(li) - i - 1): # 无序区
if li[j] > li[j+1]: # reversed 就为 降序
li[j], li[j+1] = li[j+1], li[j] # 交换
exchange = True
if not exchange:
return
return li
Select Sort (选择排序)
一趟排序记录最小的数,放到第一个位置
再一趟排序记录记录列表无序区最小的数,放到第二个位置
def select_sort(li):
for i in range(len(li) - 1): # i是第几趟
min_loc = i
for j in range(i, len(li)): # 无序区循环
if li[j] < li[min_loc]: # 判定如果小于
min_loc = j # 无序区最小的数
li[i], li[min_loc] = li[min_loc], li[i]
print(‘第%s趟‘ % i)
print(li)
时间复杂
O(n^2)
算法关键:
有序区和无序区,无序区最小数的位置
插入排序
初始时手里(有序区)只有一张牌
每次(从无序区摸一张牌,插入到手里已有牌的正确位置)
堆排序:
基础知识:
数是一种数据结构。 比如:目录结构
树是一种可以递归定义的数据结构
树是由n个节点组成的集合:
如果n = 0,那就是一颗空树
如果n > 0, 那存在1个节点作为树的根节点,其他节点可以分为m个集合,每个集合本身又是一棵树
前期概念:
根节点、叶子节点,树的深度、孩子节点、父节点、子树
堆排序前传:
完全二叉树
叶结点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树
满二叉树
一个二叉树,如果每一层的节点数都达到在最大值,则这个二叉树就是满二叉树。

父节点和左孩子节点的编号下标:
2n+1
父节点和右孩子节点的编号下标:
2n+2
堆栈
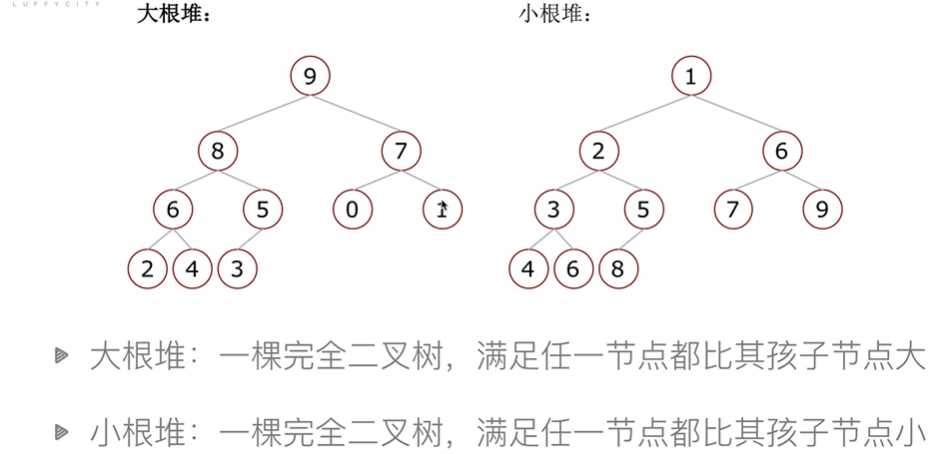
堆排序过程:
简单来说就是农村包围城市
挨个出数
def sift(li, low, high):
"""
:param li: 列表
:param low: 堆的根节点位置
:param high: 堆的最后一个元素的位置
:return:
"""
i = low # i是最开始指向的根节点
j = 2 * i + 1 # j开始是左孩子
tmp = li[low] # 把堆顶存起来
while j <= high: # tmp 和 j 的大小
if j + 1 <= high and li[j+1] > li[j]: # 如果右孩子有并且比较大
j = j + 1 # j指向右孩子
if li[j] > tmp:
li[i] = li[j]
i = j # 往下一层
j = 2 * i + 1
else:
li[i] = tmp # 把tmp放到某一级上面
break
else:
li[i] = tmp # 当tmp放到叶子节点上
def heap_sort(li):
n = len(li)
for i in range((n-2)//2, -1, -1):
sift(li, i, n-1)
# 建堆完成了
for i in range(n-1, -1, -1):
# i指向当前堆最后一个元素
li[0], li[i] = li[i], li[0]
sift(li, 0, i-1) # i-1是新的High
原文:https://www.cnblogs.com/jackson669/p/12207424.html