问题
利用sklearn中的iris(鸢尾花)数据集,选用‘sepal length (cm)‘和 ’sepal width (cm)‘这两个特征,完成感知机算法。
分析
首先我们要考虑俩个问题:
1.如何去评判感知机的好与坏
2.感知机的优化策略



下图为感知机算法流程:


原始形式代码实现
1 import numpy as np 2 import matplotlib.pyplot as plt 3 from sklearn.datasets import load_iris 4 from sklearn import datasets 5 6 7 def sign(x): 8 if x < 0: 9 return -1 10 else: 11 return 1 12 13 14 def model(w, x, b): 15 y = (-b - w[0] * x) / w[1] # 将直线转化为y=ax+b格式 16 return y 17 18 19 def fit(data): 20 learning_rate = 0.001 # 学习率 21 w = np.array([0.0, 0.0]) 22 b = 0.2 23 sumCount = 0 24 while True: 25 count = 0 26 for i in range(data.shape[0]): 27 print(f‘迭代次数:{sumCount},w: {w},b: {b}‘) 28 if data[i][-1] * sign(np.dot(w, data[i][0:2]) + b) <= 0: 29 w += data[i][0:2] * data[i][-1] * learning_rate # 根据计算得出的梯度和设定的学习率来调整w和b 30 b += data[i][-1] * learning_rate 31 count += 1 32 sumCount += 1 33 if count == 0: # 如果本轮迭代没有发现误分类点,则跳出循环 34 break 35 return w, b 36 37 38 iris = datasets.load_iris() 39 iris_data = load_iris().data 40 41 sepal_length = np.array([iris_data[i][0] for i in range(iris_data.shape[0])]) 42 sepal_width = np.array([iris_data[i][1] for i in range(iris_data.shape[0])]) 43 # sepal_length为x轴,sepal_width为y轴 44 list = [] 45 for i in range(50): # 划分数据,前50个为一组,后50个为一组 46 list.append([sepal_length[i], sepal_width[i], 1]) 47 list.append([sepal_length[50 + i], sepal_width[50 + i], -1]) 48 data = np.array(list) 49 50 plt.xlabel(‘sepal_length‘) 51 plt.xlim(4.2, 7.1) 52 plt.ylabel(‘sepal_width‘) 53 plt.ylim(1.5, 5) 54 for i in range(100): 55 if data[i][-1] == 1: 56 plt.scatter(data[i][0], data[i][1], color=‘blue‘, marker=‘*‘) 57 else: 58 plt.scatter(data[i][0], data[i][1], color=‘red‘, marker=‘o‘) 59 60 w, b = fit(data) 61 x = np.array([i for i in range(len(sepal_length))]) 62 plt.plot(x, model(w, x, b)) 63 plt.show()
分析
首先我们要考虑俩个问题:
1.如何去评判感知机的好与坏
2.感知机的优化策略
1. 在评判感知机的好与坏之前,我们需要定义感知机的模型: y=sign(![]() ·X+b),此题中的
·X+b),此题中的![]() =(
=(![]() )、X=(
)、X=(![]() ),
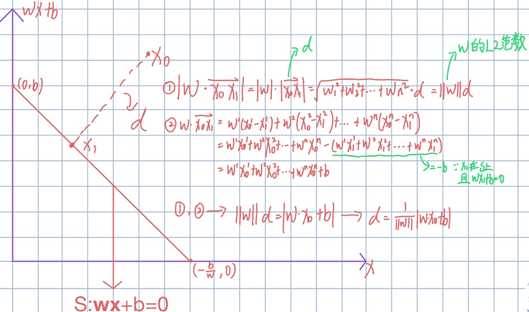
),![]() ,还需要定义感知机的损失函数,此处我们用误分类点到超平面S的总距离作为损失函数(此题中超平面即为一条分割数据的直线),下附距离推导过程,根据推导结果我们可知误分类点到S的总距离为:
,还需要定义感知机的损失函数,此处我们用误分类点到超平面S的总距离作为损失函数(此题中超平面即为一条分割数据的直线),下附距离推导过程,根据推导结果我们可知误分类点到S的总距离为:![]() ,令
,令![]() =sign(
=sign(![]() ·X+b),
·X+b),![]() ,且因为
,且因为![]() 为常数,在比较大小时俩边可以消除,所以最后损失函数为:
为常数,在比较大小时俩边可以消除,所以最后损失函数为:![]() (M为误分类点的集合)
(M为误分类点的集合)
原文:https://www.cnblogs.com/FSeng/p/12218891.html