题意:
有一个芯片,芯片上有N*N(1≤N≤40)个插槽,可以在里面装零件。 有些插槽不能装零件,有些插槽必须装零件,剩下的插槽随意。 要求装好之后满足如下两条要求:
1、第 i 行和第 i 列的零件数目必须一样多(1≤i≤N)。
2、第 i 行,第j列的零件数目不能超过总的零件数目的 A/B(1≤i≤N,0≤A≤B≤1000,B≠0)。
求最多可以另外放多少个零件(就是除掉必须放的)。如果无解输出impossible。
题解:
我们枚举每行每列最多能放的零件数目w。
设总共放了num个零件(包括必须放的)
为满足第二个限制:则w<=num*A/B
考虑第一个限制怎么办。我们可以先让所有可行的位置都放上零件,然后再把多的零件拆下来。
我们令sx[i]为第i行能放的最多零件数,sy[i]为第i列能放的最多零件数。
建图方式:
1.新增原点汇点s,t
2.由源点向每一行连流量sx[i]费用0的边。
3.每一列向汇点连流量sy[i]费用0的边。
4.每一行i向每一列i连流量w费用0的边。
5.最后对于所有可用插槽(可放可不放)ij,由第i行向第j列连容量1费 用1的边
若满流,且w<=num*A/B则为一种可行方案
原因:
若sx[i]>w,则说明流多了,但是已经流到第i行了,那就分配w的流量流向第i列,这样保证放的零件会相等,然后sx[i]-w个流量表示sx[i]-w个格子只有不选了,如果第i行第j列这个格子可以不选,那么从第i行向第j列连一条流量为1的边表示这个格子不选。为了统计这种不选的格子的数量,那么要加一个费用。
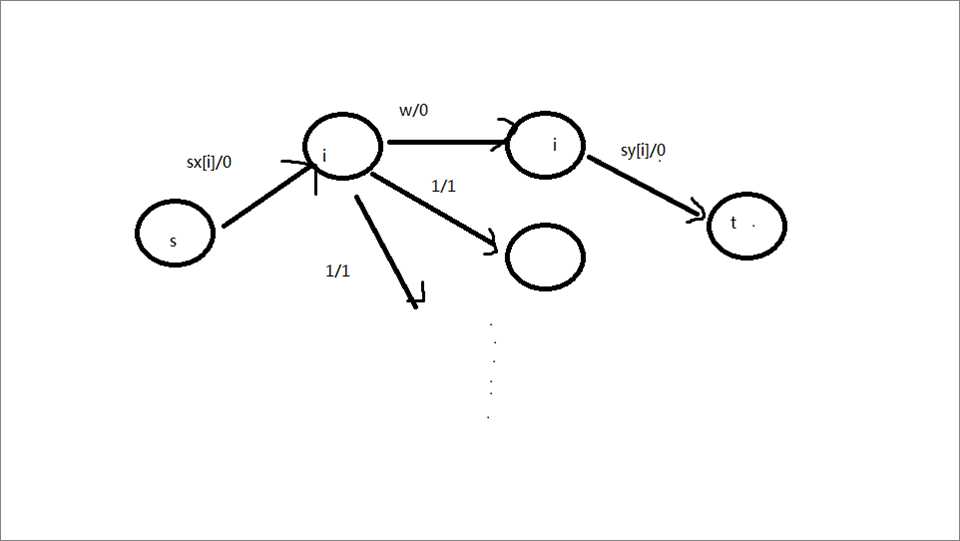
若sx[i]<=w,则直接流向第i列,不需要删除零件。
跑最小费用最大流
最后判是否满流(要符合题意),若满流则枚举的w是一个可行方案,此时总共安装的零件数量为num=∑sx[i]-拆掉的零件数(网络流的费用)
枚举所有w,求num-必须放的零件数的最大值就是答案。
顺便说一句,此题卡普通EK算法,需要一次spfa后,多路增广(多条最短路同时更新)
#pragma GCC optimize(2) #pragma GCC optimize(3) #pragma GCC optimize("Ofast") #pragma GCC optimize("inline") #include<iostream> #include<queue> #include<cstring> #include<cstdio> using namespace std; const int inf=0x7fffffff/2; struct node{int to,next,edge,c;}a[300005]; int h[105],v[105],incf[105],pre[105],d[105]; int sx[55],sy[55],in[105]; int cnt=1,n,m,s,t,maxflow,A,B,sum,used; int ans; char ch[55][55]; void add(int x,int y,int z,int c) { cnt++;a[cnt].to=y;a[cnt].edge=z;a[cnt].c=c;a[cnt].next=h[x];h[x]=cnt; cnt++;a[cnt].to=x;a[cnt].edge=0;a[cnt].c=-c;a[cnt].next=h[y];h[y]=cnt; } bool spfa() { int i,j; memset(v,0,sizeof(v)); for(i=0;i<=2*n+1;i++)d[i]=inf; queue<int> q; q.push(s);d[s]=0;v[s]=1;incf[s]=inf; while(q.size()) { int x=q.front();v[x]=0;q.pop(); for(i=h[x];i;i=a[i].next) if(a[i].edge) { j=a[i].to; if(d[j]>d[x]+a[i].c) { d[j]=d[x]+a[i].c; incf[j]=min(incf[x],a[i].edge); pre[j]=i; if(!v[j])q.push(j),v[j]=1; } } } return d[t]!=inf; } int dfs(int x,int flow) { if(x==t||!flow)return flow; int rest=0,i,j,k,dlt; in[x]=1; for(i=h[x];i&&flow;i=a[i].next) { j=a[i].to; if(!in[j]&&a[i].edge&&d[j]==d[x]+a[i].c) { dlt=dfs(j,min(flow,a[i].edge)); if(!dlt)d[j]=0; a[i].edge-=dlt; a[i^1].edge+=dlt; rest+=dlt;flow-=dlt; ans+=a[i].c*dlt; } } in[x]=0; return rest; } int check(int w) { memset(h,0,sizeof(h));cnt=1; s=0;t=2*n+1; int i,j; for(i=1;i<=n;i++) { add(s,i,sx[i],0); add(i+n,t,sy[i],0); add(i,i+n,w,0); } for(i=1;i<=n;i++) for(j=1;j<=n;j++) if(ch[i][j]==‘.‘)add(i,j+n,1,1); maxflow=0;ans=0; while(spfa())maxflow+=dfs(s,inf); if(maxflow!=sum)return -1; int num=sum-ans; if(w*B<=num*A)return num-used; else return -1; } int main() { int i,j,la=0; while(scanf("%d%d%d",&n,&A,&B)&&n+A+B) { memset(sx,0,sizeof(sx)); memset(sy,0,sizeof(sy)); sum=0;used=0; for(i=1;i<=n;i++) { scanf("%s",ch[i]+1); for(j=1;j<=n;j++) { if(ch[i][j]!=‘/‘)sx[i]++,sy[j]++,sum++; if(ch[i][j]==‘C‘)used++; } } int Ans=-1; for(i=0;i<=n;i++)Ans=max(Ans,check(i)); printf("Case %d: ",++la); if(Ans==-1)printf("impossible\n"); else printf("%d\n",Ans); } return 0; }
【BZOJ3961】[WF2011]Chips Challenge
原文:https://www.cnblogs.com/dsb-y/p/12239660.html