今天学习到二叉树的时候,看到了二叉树的先序,后序,中序遍历方法。然而二叉树遍历方法递归实现十分简单,迭代版本实现起来些许复杂,就又上手试试二叉树的各种遍历方法以及实现版本,当是温习一遍之前了解到的实现方法。
三种遍历方法中递归实现难度相当,代码相当简略。
三种遍历方法中利用栈实现的迭代版本中,先序和中序实现难度相对简单,但是后序遍历方法实现起来比较复杂,这里实现思路也不同于之前先序和中序的版本。
另外一种O(1)空间复杂度实现先序,中序实现难度也相对简单,后序相对复杂。
以下贴出完整测试代码,main函数中输入生成二叉树的方法:
输入节点数量,然后输入二叉树树形结构1,2,3,#,4其中#代表空,则1,2,3,#,4代表以下结构:
1
/ 2 3
\
4
再举一个例子,输入7个节点数量,输入1,2,3,4,5,6,7代表树形结构如下:
1
/ 2 3
/ \ / 4 5 6 7
代码:
其中_r后缀的为递归实现,_s后缀的为利用栈迭代实现,_m后缀的为O(1)空间复杂度迭代实现。
其中_m迭代实现线程不安全,因为临时的改变了树的结构。
#include <iostream>
#include <stack>
#include <vector>
using namespace std;
struct TreeNode {
int label;
TreeNode *right;
TreeNode *left;
TreeNode(int temp):label(temp) {
}
};
class Solution {
public:
void inordertraversal_r(TreeNode *root) {
if(root == NULL) {
return;
}
inordertraversal_r(root->left);
cout<<root->label<<" ";
inordertraversal_r(root->right);
}
void preordertraversal_r(TreeNode *root) {
if(root == NULL) {
return;
}
cout<<root->label<<" ";
preordertraversal_r(root->left);
preordertraversal_r(root->right);
}
void postordertraversal_r(TreeNode *root) {
if(root == NULL) {
return;
}
postordertraversal_r(root->left);
postordertraversal_r(root->right);
cout<<root->label<<" ";
}
void inordertraversal_s(TreeNode *root) {
stack<TreeNode*> s;
TreeNode *cur = root;
while(!s.empty() || cur != NULL) {
while(cur != NULL) {
s.push(cur);
cur = cur->left;
}
cur = s.top();
s.pop();
cout<<cur->label<<" ";
cur = cur->right;
}
}
void preordertraversal_s(TreeNode *root) {
stack<TreeNode*> s;
TreeNode *cur = root;
while(!s.empty() || cur != NULL) {
while(cur != NULL) {
cout<<cur->label<<" ";
s.push(cur);
cur = cur->left;
}
cur = s.top();
s.pop();
cur = cur->right;
}
}
//change thinking , it‘s too hard
void postordertraversal_s(TreeNode *root) {
//the original method
/*
We use a prev variable to keep track of the previously-traversed node. Let’s assume curr is the current node that’s on top of the stack. When prev is curr‘s parent, we are traversing down the tree. In this case, we try to traverse to curr‘s left child if available (ie, push left child to the stack). If it is not available, we look at curr‘s right child. If both left and right child do not exist (ie, curr is a leaf node), we print curr‘s value and pop it off the stack.
If prev is curr‘s left child, we are traversing up the tree from the left. We look at curr‘s right child. If it is available, then traverse down the right child (ie, push right child to the stack), otherwise print curr‘s value and pop it off the stack.
If prev is curr‘s right child, we are traversing up the tree from the right. In this case, we print curr‘s value and pop it off the stack.
*/
if(root == NULL) {
return;
}
stack<TreeNode*> s;
s.push(root);
TreeNode *cur = NULL;
TreeNode *pre = NULL;
while( !s.empty() ) {
cur = s.top();
//left down or right down
if( pre == NULL || pre->left == cur || pre->right == cur) {
if(cur->left != NULL) {
s.push(cur->left);
}
else if(cur->right != NULL) {
s.push(cur->right);
}
else {
cout<<cur->label<<" ";
s.pop();
}
}
//left up
else if(cur->left == pre) {
if(cur->right != NULL) {
s.push(cur->right);
}
else {
cout<<cur->label<<" ";
s.pop();
}
}
//right up
else if(cur->right == pre) {
cout<<cur->label<<" ";
s.pop();
}
pre = cur;
}
/* the easy method
stack<TreeNode*> s;
s.push(root);
TreeNode *cur = NULL;
TreeNode *pre = NULL;
while( !s.empty() ) {
cur = s.top();
if(pre == NULL || pre->left == cur || pre->right == cur) {
if(cur->left != NULL) {
s.push(cur->left);
}
else if(cur->right != NULL) {
s.push(cur->right);
}
}
else if(cur->left == pre) {
if(cur->right != NULL) {
s.push(cur->right);
}
}
else {
cout<<cur->label<<" ";
s.pop();
}
pre = cur;
}
*/
}
void inordertraversal_m(TreeNode *root) {
TreeNode *cur = root;
TreeNode *pre = NULL;
while(cur != NULL) {
if(cur->left == NULL) {
cout<<cur->label<<" ";
cur = cur->right;
}
else {
pre = cur->left;
while( pre->right != NULL && pre->right != cur ) {
pre = pre->right;
}
if(pre->right == NULL) {
pre->right = cur;
cur = cur->left;
}
else {
pre->right = NULL;
cout<<cur->label<<" ";
cur = cur->right;
}
}
}
}
void preordertraversal_m(TreeNode *root) {
TreeNode *cur = root;
TreeNode *pre = NULL;
while(cur != NULL) {
if(cur->left == NULL) {
cout<<cur->label<<" ";
cur = cur->right;
}
else {
pre = cur->left;
while( pre->right != NULL && pre->right != cur ) {
pre = pre->right;
}
if(pre->right == NULL) {
pre->right = cur;
cout<<cur->label<<" ";
cur = cur->left;
}
else {
pre->right = NULL;
cur = cur->right;
}
}
}
}
//this is the most difficult algorithm
void reverse_out(TreeNode *from,TreeNode *to) {
//first reverse from->to
//reverse
TreeNode *cur = from;
TreeNode *post = cur->right;
while(cur != to) {
TreeNode *tmp = post->right;
post->right = cur;
cur = post;
post = tmp;
}
//already reverse,output list
TreeNode *traversal = cur;
while( cur != from ) {
cout<<cur->label<<" ";
cur = cur->right;
}
cout<<cur->label<<" ";
//reverse original
cur = to;
post = cur->right;
while(cur != from) {
TreeNode *tmp = post->right;
post->right = cur;
cur = post;
post = tmp;
}
//restore to‘s right
to->right = NULL;
}
void postordertraversal_m(TreeNode *root) {
TreeNode *newroot = new TreeNode(0);
newroot->left = root;
newroot->right = NULL;
TreeNode *cur = newroot;
TreeNode *pre = NULL;
while(cur != NULL) {
if(cur->left == NULL) {
cur = cur->right;
}
else {
pre = cur->left;
while(pre->right != NULL && pre->right != cur) {
pre = pre->right;
}
if(pre->right == NULL) {
pre->right = cur;
cur = cur->left;
}
else {
pre->right = NULL;
reverse_out(cur->left,pre);
cur = cur->right;
}
}
}
}
};
int main(void) {
int nodecount;
while( cin>>nodecount && nodecount != 0 ) {
vector<TreeNode*> treenodes;
while(nodecount) {
nodecount--;
int nodelabel;
cin>>nodelabel;
if( ((char)nodelabel) == ‘#‘ ) {
treenodes.push_back( NULL );
}
else {
treenodes.push_back( new TreeNode(nodelabel) );
}
}
//construct the tree
for(int i = 0;i < treenodes.size();i++) {
if( treenodes[i] == NULL ) {
continue;
}
else {
//left child node 2n+1,right child node 2n+2
if( 2*i + 1 < treenodes.size() ) {
treenodes[i]->left = treenodes[2*i + 1];
}
else {
treenodes[i]->left = NULL;
}
if( 2*i + 2 < treenodes.size() ) {
treenodes[i]->right = treenodes[2*i + 2];
}
else {
treenodes[i]->right = NULL;
}
}
}
Solution s;
cout<<"inorder recursion :";
s.inordertraversal_m(treenodes[0]);
cout<<endl;
cout<<"inorder stack :";
s.inordertraversal_s(treenodes[0]);
cout<<endl;
cout<<"inorder morris :";
s.inordertraversal_r(treenodes[0]);
cout<<endl;
cout<<"preorder recursion :";
s.preordertraversal_m(treenodes[0]);
cout<<endl;
cout<<"preorder stack :";
s.preordertraversal_s(treenodes[0]);
cout<<endl;
cout<<"preorder morris :";
s.preordertraversal_r(treenodes[0]);
cout<<endl;
cout<<"postorder recursion:";
s.postordertraversal_m(treenodes[0]);
cout<<endl;
cout<<"postorder stack :";
s.postordertraversal_s(treenodes[0]);
cout<<endl;
cout<<"postorder morris :";
s.postordertraversal_r(treenodes[0]);
cout<<endl;
for(int i = 0;i < treenodes.size();i++) {
delete treenodes[i];
}
}
}
关于morris的先序,中序思路图解:
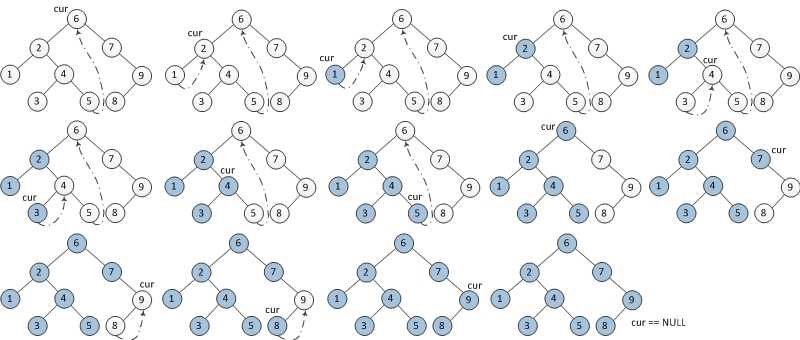
关于moriis的后序思路图解:
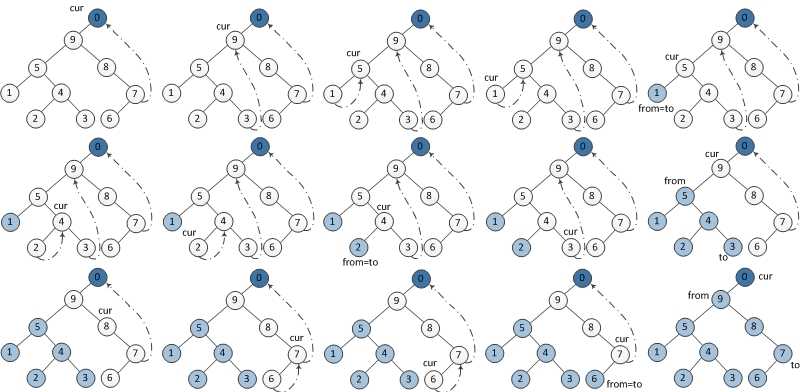
原文:http://www.cnblogs.com/weixliu/p/3945846.html