自从Lamport在1998年发表Paxos算法后,对Paxos的各种改进工作就从未停止,其中动作最大的莫过于2005年发表的Fast Paxos。无论何种改进,其重点依然是在消息延迟与性能、吞吐量之间作出各种权衡。为了容易地从概念上区分二者,称前者Classic Paxos,改进后的后者为Fast Paxos。
1. Fast Paxos概览
Lamport在40多页的论文中不仅提出了Fast Paxos算法,并且还从工程实践的角度重新描述了Paxos,使其更贴近应用场景。从一般的Client/Server来考虑,Client其实承担了Proposer和Learner的作用,而Server则扮演Acceptor的角色,因此下面重新描述了Paxos算法中的几个角色:
- Client/Proposer/Learner:负责提案并执行提案
- Coordinator:Proposer协调者,可为多个,Client通过Coordinator进行提案
- Leader:在众多的Coordinator中指定一个作为Leader
- Acceptor:负责对Proposal进行投票表决
就是Client的提案由Coordinator进行,Coordinator存在多个,但只能通过其中被选定Leader进行;提案由Leader交由Server进行表决,之后Client作为Learner学习决议的结果。
这种方式更多地考虑了Client/Server这种通用架构,更清楚地注意到了Client既作为Proposer又作为Learner这一事实。
同样要注意到的是,如果Leader宕机了,为了保证算法的正确性需要一个Leader的选举算法,但与之前一样,Lamport并不关心这个Leader选举算法,他认为可以简单地通过随机或超时机制实现。
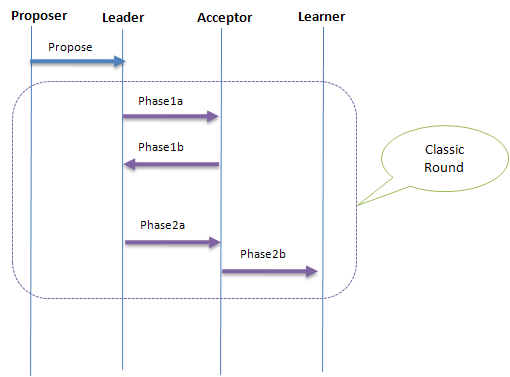
另外在Classic Paxos中,从每次Proposer提案到决议被学习,需要三个通信步骤:
Proposer-----Leader-----Acceptor-----Learner
从直观上来说,Proposer其实更“知道”提交那个Value,如果能让Proposer直接提交value到Acceptor,则可以把通信步骤减少到2个。Fast Paxos便是基于此而产生。
2. Make Paxos Faster
我们再回顾下Classic Paxos的几个阶段:
- Phase1a:Leader提交proposal到Acceptor
- Phase2b:Acceptor回应已经参与投票的最大Proposer编号和选择的Value
- Phase2a:Leader收集Acceptor的返回值
Phase2a.1:如果Acceptor无返回值,则自由决定一个
Phase2a.2: 如果有返回值,则选择Proposer编号最大的一个
- Phase2b:Acceptor把表决结果发送到Learner
很明显,在Phase2a.1中,如果Leader可以自由决定一个Value,则可以让Proposer提交这个Value,自己则退出通信过程。只要之后的过程运行正常,Leader始终不参与通信,一直有Proposer直接提交Value到Acceptor,从而把Classic Paxos的三阶段通信减少为两阶段,这便是Fast Paxos的由来。因此,我们更加形式化下Fast Paxos的几个阶段:
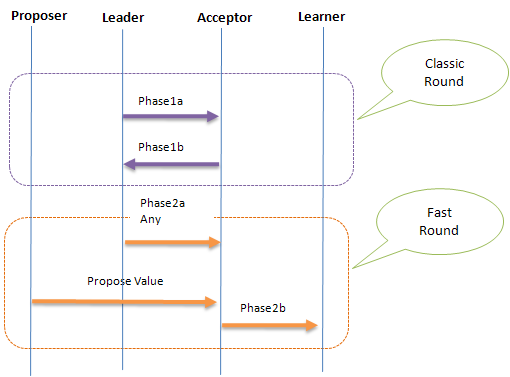
- Phase1a:与之前相同
- Phase1b:与之前相同
- Phase2a:Leader收集Acceptor的返回值
Phase2a.1:如果Acceptor无返回值,则发送一个Any消息给Acceptor,之后Acceptor便等待Proposer提交Value
Phase2a.2:如果有返回值,则根据规则选取一个
- Phase2b:Acceptor把表决结果发送到Learner(包括Leader)
算法主要变化在Phase2a阶段,即:
- 若Leader可以自由决定一个Value,则发送一条Any消息,Acceptor便等待Proposer提交Value
- 若Acceptor有返回值,则Acceptor需选择某个Value
先不考虑实现,从形式上消息仅需在Proposer-----Acceptor-----Learner之间传递即可,也即仅需2个通信步骤。下面我们详细说明算法过程:
3 一些定义
- Quorum
在Classic Paxos中一直通过多数派(Majority)来保证算法的正确性,对多数派再进一步抽象化,称为“Quorum”,要求任意两个Quorum之间有交集(从而间接表达了majority的含义)
- Round
在Classic Paxos中,Proposer每次提案都用一个全序的编号表示,如果执行顺利,该编号的Proposal在经历Phase1,Phase2后最终会执行成功。
在Fast Paxos称这个带编号的Proposal的执行过程为“Round”
- i-Quorum
在Classic Paxos执行过程中,一般不会明确区分每次Round执行的Quorum,虽然也可以为每个Round指定一个Quorum。在Fast Paxos中会通过i-Quorum明确指定Round i需要的Quorum
- Classic Round
执行Classic Paxos的Round称为Classic Round
- Fast Round
如果Leader发送了Any消息,则认为后续通信是一个Fast Round;若Leader未发送Any消息,还是跟之前一样通信,则后续行为仍然是Classic Round。
根据Lamport描述,Classic Round和Fast Round可通过Round Number进行加以区分。
4 Any消息
在正常情况下,Leader若可以自由决定一个Value,应该发生一条Phase2a消息,其中包含了选择的Value,但此时却发送了一条无Value的Any消息。Acceptor在接收到Any消息后可做一些开始Fast Round的初始化工作,等待Proposer提交真正的Value。Any消息的意思是Acceptor可以做任意的处理。
因此,一个Fast Round包括两个阶段:由Any消息开始的阶段,和由Proposer提交Value的结束阶段,而Leader只是起到一个初始化过程的作用,如果没有错误发生,Leader将退出之后的通信中过程。
下面是Classic Paxos交互图:
下面是Fast Paxos的交互图:
5 冲突
在Classic Paxos中,Acceptor投票的value都是Leader选择好的,所以不存在同一Round中投票多个Value的场景,从而保证了一致性。但在Fast Round中因为允许多个Proposer同时提交不同的Value到Acceptor,这将导致在Fast Round中没有任何value被作为最终决议,这也称为“冲突”(Collision)
Proposer提交的Round是全序的,不同的Proposer提交的Round肯定不一样,同一Proposer不可能在同一Round中提交不同的Value,那为什么还会有同一Fast Round中有多个Value的情况?原因在于Fast Round与Round区别,当Fast Round开始后,会被分配一个唯一的Round Number,之后无论多少个Proposer提交Value都是基于这个Round Number,而不管Proposer提交的Round是否全序。
比如,Fast Round Number为10,Proposer1提交了(11,1),Proposer2提交了(12,2),但对Fast Round来说存在(10,1,2)两个Value。
因为冲突的存在,会导致Phase2a.2的选择非常困难,原因是:
在Classic Paxos中,如果Acceptor返回多个Value,只要排序,选择最高的编号对应的Value即可,因为Classic Paxos中的Value都是有Leader选择后在Phase2a中发送的,因此最高编号的Value肯定只有一个。但在Fast Paxos中,最高编号的Value会发现多个,比如(10,1,2)。
假如当前Leader正在执行第i个Classic Round(i-Quorum为Q) ,得到Acceptor反馈的最高编号为k,有两个value:v、w,说明Fast Round k存在两个k-Quorum,Rv,Rw。
O4(v):下面定义在Round k中v或w被选择的条件:
如果v在Round k中被选择,那么存在一个k-Quorum R,使得对任意的Acceptor a∈Q∩R,都对v作出投票。
这个问题也可表述为:R中的所有Acceptor都对v作出投票,并且Q∩R≠φ,因为如果Q∩R=φ,则Round i将无法得知投票结果
因此如果保证下面两个条件:
- 每个Acceptor在同一Fast Round中仅投票一个Value
- Q∩Rv∩Rw≠φ
则v、w不可能同时被选择
6 确定Quorum
根据上面描述,为了防止一次Fast Round选择多个Value,Quorum需要满足下面两个条件:
- 任意两个Classic Quorum有交集
- 任意一个Classic Quorum与任意两个Fast Quorum有交集
不妨设总Acceptor数为N,Classic Round运行的最大失败Acceptor数为F,Fast Round允许的失败数为E,即N-F构成Classic Round的一个Quorum,N-E构成Fast Round的一个Quorum。
上面两个条件等价于:
设Qc,Qf分别为Classic和Fast Round的Quorum大小,经过整理可得两个下限结果:
- |Qc| = |Qf| ≥ N − ⌈N/3⌉ + 1 ≥ ⌊2N/3⌋ + 1
- |Qc| ≥N-⌈N/2⌉+1 = ⌈N/2⌉+1
|Qf|≥N-⌈N/4⌉≥⌈3N/4⌉
证明请参考:
一致性算法中的节点下限7 冲突Recovery
作为优化,Acceptor在投票Value时也应该发送到Leader,这样Leader就很容易能发现冲突。Leader如果在Round i发现冲突,可以很容易地开始Roun i+1,从Phase1a开始重新执行Classic Paxos过程,但这个其实可以进一步优化,我们首先考虑下面这个事实:
如果Leader重启了Round i+1,并且收到了i-Quorum个Acceptor发送的Phase1b消息,则该消息明确了两件事情:
- 报告Acceptor a参与投票的最大Round和对应的Value
- 承诺不会对小于i+1的Round作出投票
假如Acceptor a也参与了Round i的投票,则a的Phase1b消息同样明确了上述两件事情,并且会把对应的Round,Value在Phase2b中发送给Leader(当然还有Learner),一旦Acceptor a执行了Phase2b,则也同时表明a将不会再对小于i+1的Round进行投票。
也就是说,Round i的Phase2b与Round i+1的Phase1b有同样的含义,也暗含着如果Leader收到了Round i的Phase2b,则可直接开始Round i+1的Phase2a。经过整理,产生了两种解决冲突(Recovery)的方法:
7.1 基于协调者的Recovery
如果Leader在Round i 中收到了(i+1)-Quorum个Acceptor的Phase2b消息,并且发现冲突,则根据O4(v)选取一个value,直接执行Round i+1的Phase2a;否则,从Phase1a开始重新执行Round i+1
7.2 基于非协调的Recovery
作为基于协调Recovery的扩展,非协调要求Acceptor把Phase2b消息同时发送给其他Quorum Acceptor,由每个Acceptor直接执行Round i+1的Phase2a,但这要求i-Quorum与(i+1)-Quorum必须相同,并且遵循相同选择value的规则。
这种方式的好处是Acceptor直接执行Round i+1的Phase2a,无需经过Leader,节省了一个通信步骤,缺点是Acceptor同时也作为Proposer,搞的过于复杂。
8 Fast Paxos Progress
至此,再完整地总结下Fast Paxos的Progress:
- Phase1a:与之前相同
- Phase1b:与之前相同
- Phase2a:Leader收集Acceptor的返回值
Phase2a.1:如果Acceptor无返回值,则发送一个Any消息给Acceptor,之后Acceptor便等待Proposer提交Value
Phase2a.2:如果有返回值
2.1 如果仅存在一个Value,则作为结果提交
2.2 如果存在多个Value,则根据O4(v)选取符合条件的一个
2.3 如果存在多个结果并且没有符合O4(v)的Value,则自由决定一个
- Phase2b:Acceptor把表决结果发送到Learner(包括Leader)
9. 总结
Fast Paxos基本是本着乐观锁的思路:如果存在冲突,则进行补偿。其中Leader起到一个初始化Progress和解决冲突的作用,如果Progress一直执行良好,则Leader将始终不参与一致性过程。
因此Fast Paxos理论上只需要2个通信步骤,而Classic Paxos需要3个,但Fast Paxos在解决冲突时有至少需要1个通信步骤,在高并发的场景下,冲突的概率会非常高,冲突解决的成本也会很大。
另外,Fast Paxos把Client深度引入算法中,致使其架构远没Classic Paxos那么清晰,也没Classic Paxos容易扩展。
还有一点要注意的是,Fast Quorum的大小比Classic的要大,一般Fast Quorum至少需要4个节点(3E+1),而Classic Paxos需要3个(2F+1)(请参考:
一致性算法中的节点下限)。
总之,在我看来Fast Paxos是一个理论上可行,但实际中很难操作的算法,实际中用的比较多的还是Classic Paxos的各种简化形式
10 参考资料
转自:http://blog.csdn.net/chen77716/article/details/7297122
Fast Paxos(转)
原文:http://www.cnblogs.com/javaleon/p/3945868.html