基本思想是利用迭代点\(x_k\)处的一阶导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似,然后把二次模型的极小点作为新的迭代点,并不断重复这一过程,直至求得满足精度的近似极小值。
对于f(x)=0,求解x;
初始化\(\theta\) ,然后一直迭代:\(\theta^{(t+1)}=\theta^{(t)}-\frac{f(\theta^{(t)})}{f^`(\theta^{(t)})}\)
收敛的很快;二次收敛;
牛顿法也被用于求函数的极值。由于函数取极值的点处的导数值为零,故可用牛顿法求导函数的零点,其叠代式为 ;\(\theta^{(t+1)}=\theta^{(t)}-\frac{f^`(\theta^{(t)})}{f^{``}(\theta^{(t)})}\)
如果变量是一个向量则:\(\theta^{(t+1)}=\theta^{(t)}-H^{-1}\bigtriangledown_\theta L\) 其中H是Hessian矩阵,\(H_{ij}=\frac{\partial^2L}{\partial\theta_i\partial\theta_j}\)
缺点:每次迭代都得重新计算一次H;
\(p(y;\eta)=b(y)exp(\eta^TT(y)-a(\eta))\) 其中\(\eta:分布的自然参数(规范参数)\) ,T(y):充分统计量(一般都等于y),\(a(\eta)\) :是对数划分函数,\(e^{-a(\eta)}充当正规化常量的作用,保证\sum p(y;\eta)=1\)。
固定T,a,b;定义一簇以\(\eta\) 为参数的分布,随着它的改变,可以得到不同的分布。
分别以伯努利(Bernoulli)分布和高斯(Gauss)分布为例子;
已知:p(y=1;\(\phi\))=\(\phi\) ;p(y;\(\phi\))=\(\phi^y(1-\phi)^{1-y}=exp(ylog\phi+(1-y)log(1-\phi))=exp((log(\frac{\phi}{1-\phi}))y+log(1-\phi))\)
对应可得:\(\eta=log(\frac{\phi}{1-\phi}),反向求\phi=\frac{1}{1+e^{-\eta}},带入其中,得a(\eta)=-log(1-\phi)=log(1+e^\eta)\)
b(y)=1;
一般都令\(\sigma=0\),因为它无用
\(p(y;u)=\frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2}(y-\mu)^2)=\frac{1}{\sqrt{2\pi}}exp(-\frac{1}{2}y^2)exp(-\frac{1}{2}\mu^2)\)
对应得:
\(\eta=\mu;a(\eta)=\mu^2/2=\eta^2/2;b(y)=(\frac{1}{\sqrt{2\pi}})exp(-y^2/2)\)
线性回归中我们假设:y|x;\(\theta\) ~ \(N(\mu,\sigma^2)\)
逻辑回归中我们假设:y|x;\(\theta\) ~ \(Bernoulli(\phi)\)
它们都是广义线性模型的特例。
Assume:
(1)y|x;\(\theta\) ExponentiaFamily(\(\theta\)) 给定样本xx与参数θθ,样本分类yy?服从指数分布族中的某个分布;
(2)given x, goal is to output E[T(y)|x], want h(\(\theta\)(x))=E[T(y)|x];
(3)\(\eta=\theta^Tx\) 。
3.1Gauss(\(\mu,\theta\)):\(h_\theta(x)=E[y|x;\theta]=\mu=\eta=\theta^Tx\)
\(3.2Ber(\phi)\) :\(h_\theta(x)=E[y|x]=p(y=1|x;\theta)=\phi=\frac{1}{1+e^{-\eta}}=\frac{1}{1+e^{-\theta^Tx}}\)
总之,广义线性模型通过拟合响应变量的条件均值的一个函数(不是响应变量的条件均值),并假设响应变量服从指数分布族中的某个分布(不限于正态分布),从而极大地扩展了标准线性模型。模型参数估计的推导依据是极大似然估计,而非最小二乘法。
\(y\in\{1,..,k\}\) ,每种分类的概率:\(\phi_1,...,\phi_k\) ,他们的和为1,所以一般用k-1个参数
\(p(y=i)=\phi_i\) ;
这里T(y)\(\in R^{k-1}\) ,它是一个k-1维的向量,依次从只有第1个为0,...,只有第k-1给为0,全为0。一共k种取值。
指示函数:1{True}=1,1{False}=0; 所以\(T(y)_i=1\{y=i\}\)
得到
\[ \begin{align}p(y;\phi)=&\phi_1^{1\{y=1\}}\phi_1^{1\{y=1\}}...\phi_k^{1\{y=k\}} \\=&\phi_1^{T(y)_1}\phi_2^{T(y)_2}...\phi_k^{1-\sum_{i=1}^{k-1}(T(y))_i}\\=&exp((T(y))_1log(\phi_1)+(T(y))_2log(\phi_2)...+(1-\sum_{i=1}^{k-1}(T(y))_i)log(\phi_k))\\=&b(y)exp(\eta^TT(y)-a(\eta))\end{align} \]
其中\(\eta=\left[\begin{matrix} log(\frac{\phi_1}{\phi_k}) \\ log(\frac{\phi_1}{\phi_k}) \\...\\log(\frac{\phi_{k-1}}{\phi_k}) \\\end{matrix}\right] , a(\eta)=-log(\phi_k) ,b(y)=1\)
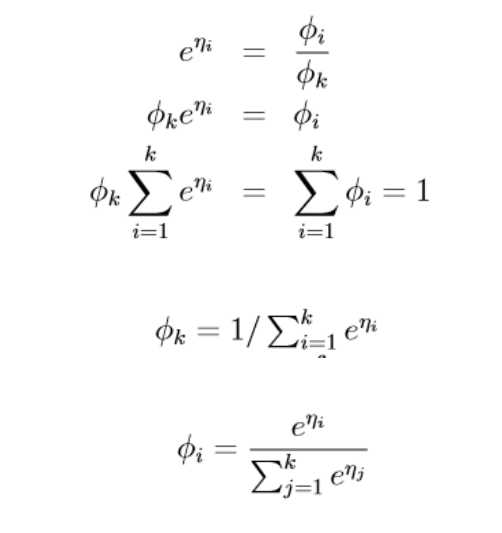
所以\(p(y=i|x;\theta)=\phi_i=\frac{e^{\eta_i}}{sum_{j=1}{k}}=\frac{e^{\theta_i^Tx}}{\sum_{j=1^k}e^{\theta_j^Tx}}\)
然后通过广义模型求解:
\(h_\theta(x)=E[T(y)|x;\theta]=E\left[ \begin{matrix} 1\{ y=1\} \\1\{ y=2\} \\...\\1\{ y=k-1\} \\ \end{matrix} |x;\theta \right]=\phi_{k-1}=\frac{exp(\theta_{k-1}^Tx)}{\sum_{j=1}^kexp(\theta_j^Tx)}\)
此后再用之前的最大似然法拟合参数即可
原文:https://www.cnblogs.com/daizigege/p/12243987.html