已知,
\[ \Delta y(t) = \begin{cases} \Delta y(t_{first}) & t \le t_{first}\\Delta y(t_{last}) & t \ge t_{last}\\alpha \Delta y(t_{left}) + (1-\alpha) \Delta y(t_{right})& \text{ else} \end{cases} \]
\[ \alpha = \frac{t_{right}-t}{t_{right} - t_{left}} \]
\[ t_{left} < t < t_{right} \]
求解 \(CF_{left}\)、\(CF_{right}\) 和 \(CF_0\) 使得:
\[ \begin{aligned} P &= \frac{CF_t}{e^{y(t)t}} \&= \frac{CF_{left}}{e^{y(t_{left})t_{left}}} + \frac{CF_{right}}{e^{y(t_{right})t_{right}}} + CF_0 \end{aligned} \tag{1} \]
要求关键利率久期不变,那么:
\[ \begin{aligned} \frac{1}{P} \frac{\partial P}{\partial y(t_{left})} &=\frac{1}{P} \frac{\partial P}{\partial y(t)} \frac{\partial y(t)}{\partial y(t_{left})}\&\approx\frac{1}{P} \frac{\partial P}{\partial y(t)} \frac{\Delta y(t)}{\Delta y(t_{left})}\&\approx-\frac{1}{P} \frac{CF_t\times t}{e^{y(t)t}} \alpha\&=-t\alpha \\frac{1}{P} \frac{\partial P}{\partial y(t_{left})} &=\frac{1}{P} \frac{\partial \left(\frac{CF_{left}}{e^{y(t_{left})t_{left}}} + \frac{CF_{right}}{e^{y(t_{right})t_{right}}} + CF_0 \right) }{\partial y(t_{left})}\&=-\frac{1}{P} \frac{CF_{left}\times t_{left}}{e^{y(t_{left})t_{left}}} \end{aligned} \]
解出
\[ CF_{left} = \frac{t \alpha P e^{y(t_{left})t_{left}}}{t_{left}} \tag{2} \]
同理解出
\[ CF_{right} = \frac{t (1-\alpha) P e^{y(t_{right})t_{right}}}{t_{right}} \tag{3} \]
(2)和(3)代入(1)解出
\[ CF_0 = P \times \frac{(t-t_{left})(t-t_{right})}{t_{left} \times t_{right}} \]
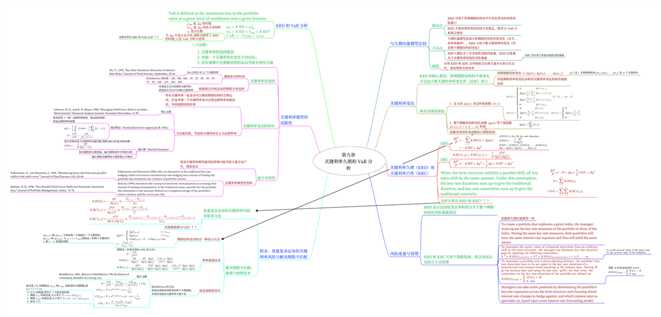
《Interest Rate Risk Modeling》阅读笔记——第九章:关键利率久期和 VaR 分析
原文:https://www.cnblogs.com/xuruilong100/p/12244274.html