请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。 路径可以从矩阵中任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。
例如在下面的3×4的矩阵中包含一条字符串“BFCE”的路径(路径中的字母用下划线标出)。但矩阵中不包含字符串“ABFB”的路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。
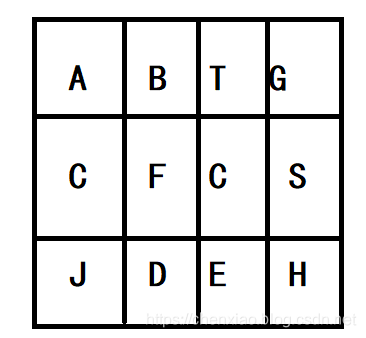
题意比较容易理解,场景也比较直观,没有需要特别考虑的地方。
一般而言,暴力穷举是可以实现的,把穷举的结果封装成字典树,直接查即可。但是如果不提前知道字符串中的字符的位数,需要考虑所有位数可能的情况,那么代价是非常非常大的,情况实在是太多了。
既然要暴力,那这里比较好的迂回方案是 回溯法, 我比较喜欢称它““温柔的暴力”
回溯法的基本做法说白了就是搜索,或是一种组织得井井有条的,能避免不必要搜索的穷举式搜索法,这种方法适用于解一些组合数相当大的问题。回溯法在问题的解空间树中,按深度优先策略,从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时,先判断该结点是否包含问题的解。如果肯定不包含,则跳过对该结点为根的子树的搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按深度优先策略搜索。
用回溯法解题的一个显著特征是在搜索过程中动态产生问题的解空间。在任何时刻,算法只保存从根结点到当前扩展结点的路径。
基本思想如下:
针对所给问题,定义问题的解空间;
确定易于搜索的解空间结构;
以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索
剪枝函数有下面两种常见的类型:
- 用
约束函数在扩展结点处剪去不满足约束的子树;- 用
限界函数剪去得不到最优解的子树。
下面依据算法思想去分析这个问题:
假如从 F 开始,我们下一步有 4 种搜索可能,如果先搜索 D,需要将 D 标记为已经使用,防止重复使用。在这一次搜索结束之后,需要将 D 的已经使用状态清除,并搜索 B。
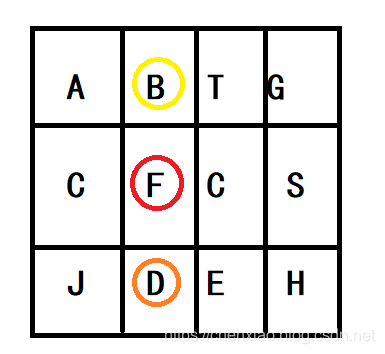
代码如下:
/**
*
* @param matrix 字符数组
* @param rows 矩阵的行数
* @param cols 矩阵的列数
* @param str 查找的字符串的字符数组
* @return 判断结果
*/
public boolean hasPath(char[] matrix, int rows, int cols, char[] str) {
if (matrix == null || rows < 1 || cols < 1 || str == null) {
return false;
}
// 用于记录状态的数组 默认为false,也就是没有访问过
boolean[] isVisited = new boolean[rows * cols];
Arrays.fill(isVisited, false);
// pathLength记录已经搜索时的字符串长度
int pathLength = 0;
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
if (hasPathCore(matrix, rows, cols, row, col, str, pathLength, isVisited))
return true;
}
}
return false;
}
// 解空间
private boolean hasPathCore(char[] matrix, int rows, int cols, int row, int col, char[] str, int pathLength,
boolean[] isVisited) {
// 剪枝 并回溯
if (row < 0 || col < 0 || row >= rows || col >= cols || isVisited[row * cols + col]
|| str[pathLength] != matrix[row * cols + col]) {
return false;
}
// 判断是否满足结束条件
if (pathLength == str.length - 1) {
return true;
}
// 记录元素已经被访问
isVisited[row * cols + col] = true;
boolean hasPath = hasPathCore(matrix, rows, cols, row - 1, col, str, pathLength + 1, isVisited)
|| hasPathCore(matrix, rows, cols, row + 1, col, str, pathLength + 1, isVisited)
|| hasPathCore(matrix, rows, cols, row, col - 1, str, pathLength + 1, isVisited)
|| hasPathCore(matrix, rows, cols, row, col + 1, str, pathLength + 1, isVisited);
// 不满足(但是可能之后满足,这里消除已访问状态)
if (!hasPath) {
isVisited[row * cols + col] = false;
}
// 回溯
return hasPath;
}如果对递归不熟悉,这套题又有点陌生。那你看是有点难看出来门道的,动笔画画,用IDE调试一下,才能理解更好点。
这里需要说明一下:回溯是深度优先搜索的一种特例,它在一次搜索过程中需要设置一些本次搜索过程的局部状态,并在本次搜索结束之后清除状态。而普通的深度优先搜索并不需要使用这些局部状态,虽然还是有可能设置一些全局状态。
记得当年,我第一次接触回溯法的时候,对解空间非常懵。这里记录一下,我是如何认识解空间的。
解空间 是 解的空间结构的意思。
对于问题的解的空间结构通常以树或图的形式表示,比较常见的两类典型的解空间是子集树和排列树。
当所给的问题是从n个元素的集合S中找到S满足某种性质的子集时,相应的解空间树称为子集树。我们上面做的这道题用到的解空间就是子集树。
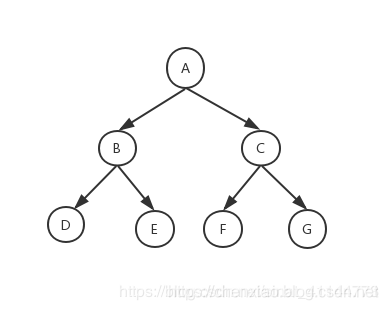
上图是一棵n为3的子集树。从根到每一个叶结点的路径表示一个可行解。从根结点出发,以深度优先的方式搜索整棵树。用回溯法搜索子集树的一般算法 伪代码 可描述为:
void backtrack(int t)
{
// t表示递归深度,表示树的第t层。
if(t > n) { // 当t > n时,算法已搜索到叶结点
output(x); // output( x ) 输出可行解
}
else {
for(int i = 0; i <= 1; i++) {
// 否则,记录当前选择的x的值(即0或1)
x[t] = i;
// 并递归遍历所有子树
// (constraint(t) && bound(t)) 表示剪枝函数,只有满足剪枝函数的子树才继续递归
if(constraint(t) && bound(t)) {
backtrack(t+1);
}
}
}当所给问题是确定n个元素满足某种性质的排列时,相应的解空间树称为排列树。排列树从根到叶结点表示一条可选路径。与子集树不同的是,每一个当前结点的搜索策略是选择剩下的元素中的一个,而子集树是选择或不选择当前元素。排列树通常有n!个叶子节点。因此遍历排列树需要O(n!)的计算时间。
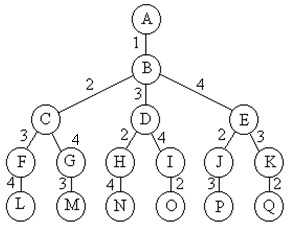
(图示为旅行员售货)
用回溯法搜索排列树的一般算法为(伪代码 参考旅行员售货问题):
void backtrack(int t)
{
if(t > n) {
output(x);
}
else//与子集树不同,搜索 剩下的结点
{
for(int i = t; i <= n; i++) {
swap(x[t], x[i]);
if(constraint(t)&&bound(t)) {
backtrack(t+1);
}
swap(x[t], x[i]);
}
}原文:https://www.cnblogs.com/JefferyChenXiao/p/12246291.html