本题要求本质不同的子矩阵,即位置不同也算相同(具体理解可以看样例自己yy)。
我们先看自己会什么,我们会求一个字符串中不同的子串的个数。我们考虑把子矩阵变成一个字符串。
先枚举矩阵的宽度,记为w(1<=w<=m)。再把一行之内的连续的w的字符用字符串hash哈成一个整数,再把这个整数hash成一个较小的数(相当于之前字符串的一个字符)。
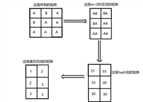
把最后完成的矩阵在把没一列接起来,形成一个字符串(每列后要加一个字符如:1 2 3 4 2 3 3 5)。然后对这个串求我们会的子串个数(减去height值)即可。
#include <iostream> #include <cstdio> #include <map> using namespace std; typedef long long ll; typedef unsigned long long ull; const ll N = 120, M = 120; const ull P = 13331; ll len, tot, ans; ll n, m; ll s[N * M], rnk[N * M], sa[N * M], sum[N * M], v1[N * M], v2[N * M], height[N * M]; char arr[N][M]; ull _hash[N][M]; map<ull, ll> mp; bool cmp(ll *t, ll a, ll b, ll l) { return t[a] == t[b] && t[a + l] == t[b + l]; } void da() { ll i, j, p = 0; for (i = 1; i <= tot; i++) sum[i] = 0; for (i = 1; i <= len; i++) sum[rnk[i] = s[i]]++; for (i = 2; i <= tot; i++) sum[i] += sum[i - 1]; for (i = len; i >= 1; i--) sa[sum[rnk[i]]--] = i; for (j = 1; j <= len; j *= 2, tot = p) { for (p = 0, i = len - j + 1; i <= len; i++) v2[++p] = i; for (i = 1; i <= len; i++) if (sa[i] > j) v2[++p] = sa[i] - j; for (i = 1; i <= len; i++) v1[i] = rnk[v2[i]]; for (i = 1; i <= tot; i++) sum[i] = 0; for (i = 1; i <= len; i++) sum[v1[i]]++; for (i = 2; i <= tot; i++) sum[i] += sum[i - 1]; for (i = len; i >= 1; i--) sa[sum[v1[i]]--] = v2[i]; for (swap(rnk, v2), rnk[sa[1]] = 1, i = 2, p = 2; i <= len; i++) { rnk[sa[i]] = cmp(v2, sa[i - 1], sa[i], j) ? p - 1 : p++; } } } void calheight() { ll i, j, p = 0; for (i = 1; i <= len; i++) { if (p) p--; j = sa[rnk[i] - 1]; while (s[i + p] == s[j + p]) p++; height[rnk[i]] = p; } } ull ksm[150]; int main() { ksm[0] = 1; for (int i = 1; i <= 130; i++) { ksm[i] = ksm[i - 1] * P; } scanf("%lld%lld", &n, &m); for (ll i = 1; i <= n; i++) { scanf("%s", arr[i] + 1); for (ll j = 1; j <= m; j++) { _hash[i][j] = _hash[i][j - 1] * P + arr[i][j] - ‘A‘ + 1; } } for (ll w = 1; w <= m; w++) { tot = 0, len = 0; mp.clear(); for (ll j = 1; j + w - 1 <= m; j++) { for (ll i = 1; i <= n; i++) { ull tmp = _hash[i][j + w - 1] - _hash[i][j - 1] * ksm[w]; if (mp[tmp] == 0) { mp[tmp] = ++tot; } s[++len] = mp[tmp]; } s[++len] = ++tot; } da(); calheight(); ans += n * (n + 1) / 2 * (m - w + 1); for (ll i = 2; i <= len; i++) { ans -= height[i]; } } cout << ans; return 0; }
Samjia 和矩阵[loj6173](Hash+后缀数组)
原文:https://www.cnblogs.com/zcr-blog/p/12246446.html