[数学]Euler‘s Method 欧拉方法

1-思想原理

求解一阶的常微分方程ODE，欧拉想出一种数值方法，得到一种线性近似Linear approximation
他并非求解出具体的y的方程，而是根据给定的初始值\((x_0,y_0=f(x_0)\)求得下个想要求得的点\(x_n\)的函数值\(y_n=f(x_0)\)，当然这样就得到了想要的点的坐标\((x_n,y_n=f(x_n)\)。
那么他是怎么做的呢？
欧拉是利用倒数的几何意义即斜率来求得下个点的坐标值
欧拉说 下个点的函数值近似等于 \[y_n = y_0 + \frac{dy}{dx}|_{x=x_0} * (x_n-x_0)\]
欧拉是借鉴了 这样的一个事实： \[\frac{y_1-y_0}{x_1-x_0}=tan\alpha\]
欧拉说如果\(h=x_1-x_0\)足够小，那么就结果值越精确

2-案例

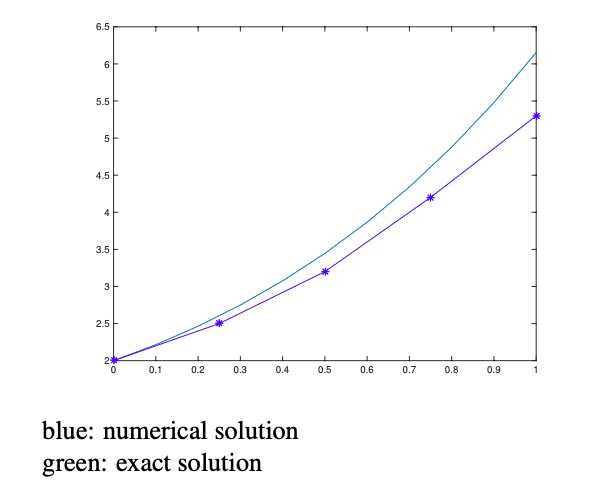
下图是一个example，初始值为(0,2)，求得在区间[0,1]上的函数值，分成等长的四段，每段长0.25，这里就体现了线性近似(看结果图)

对比图

MATLAB 代码

fun = @(x,y) (x+y);

% 欧拉近似值
re = euler_method(fun,0,2,1,0.25);
fprintf('result is %f\n',re);

% 准确值
xx = 0:0.25:1;
yy = 3*exp(xx)-xx-1;
plot(xx,yy,'b');

% Euler Method
% f 表示一阶常微分方程
% (x0,y0):初始值
% xn要求的函数值的自变量的值
% h 步长
function y = euler_method(f,x0,y0,xn,h)
    n = round((xn-x0)/h);
    y = y0;
    x = x0;
    xa = [];
    xa(1) =x0;
    re = [];
    re(1) = y;
    
    for i=1:n
        y = y + h*f(x,y);
        x = x + h;
        % 保存段点值，用于绘图
        xa(i+1)=x;
        re(i+1)=y;
    end  
    plot(xa,re,'r');
    hold on;%不清除画面
    scatter(xa,re,'*');% 描点
    
end

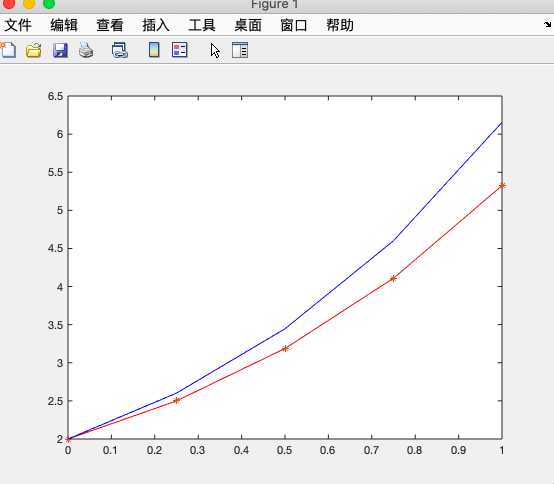
Result:

[数学]Euler‘s Method 欧拉方法

原文：https://www.cnblogs.com/tailiang/p/12246792.html