1.逻辑斯谛回归
（logistic regression） 是统计学习中的经典分类方法。 最大熵是概率模型学习的一个准则， 将其推广到分类问题得到最大熵模型（maximum entropy model） 。逻辑斯谛回归模型与最大熵模型都属于对数线性模型。本文只介绍逻辑斯谛回归。
设X是连续随机变量， X服从Logistic distribution，
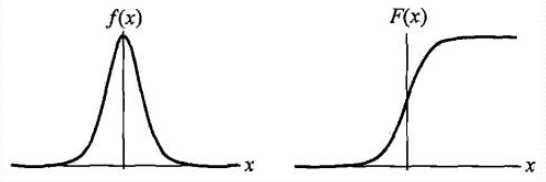
分布函数：
密度函数：
μ为位置参数， γ大于0为形状参数， (μ,1/2)中心对称
Sigmoid：
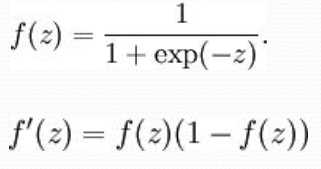
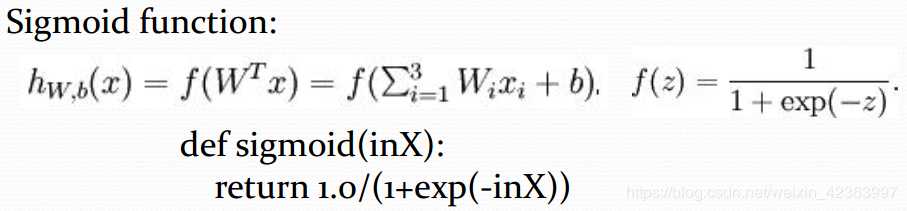
双曲正切函数（tanh）：
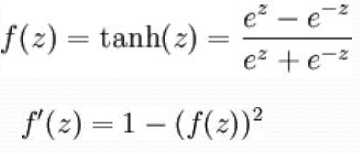
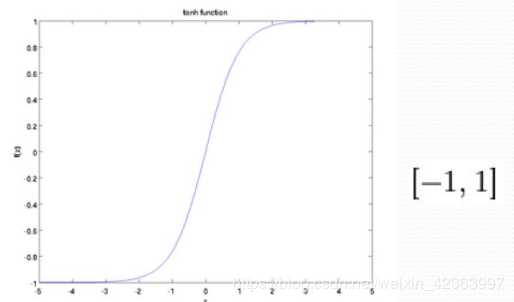
2.二项逻辑斯蒂回归
Binomial logistic regression model
由条件概率P(Y|X)表示的分类模型
形式化为logistic distribution
X取实数， Y取值1,0
事件的几率odds： 事件发生与事件不发生的概率之比为称为
事件的发生比(the odds of experiencing an event),
对数几率：
对逻辑斯蒂回归：
3.似然函数
logistic分类器是由一组权值系数组成的， 最关键的问题就是如何获取这组权值， 通过极大似然函数估计获得， 并且
Y~f(x;w)
似然函数是统计模型中参数的函数。 给定输出x时， 关于参数θ的似然函数L(θ|x)（在数值上） 等于给定参数θ后变量X的概率： L(θ|x)=P(X=x|θ)
似然函数的重要性不是它的取值， 而是当参数变化时概率密度函数到底是变大还是变小。
极大似然函数： 似然函数取得最大值表示相应的参数能够使得统计模型最为合理。
那么对于上述m个观测事件， 设
其联合概率密度函数， 即似然函数为：
目标： 求出使这一似然函数的值最大的参数估， w1,w2,…,wn，使得L(w)取得 最大值。
对L(w)取对数。
对数似然函数
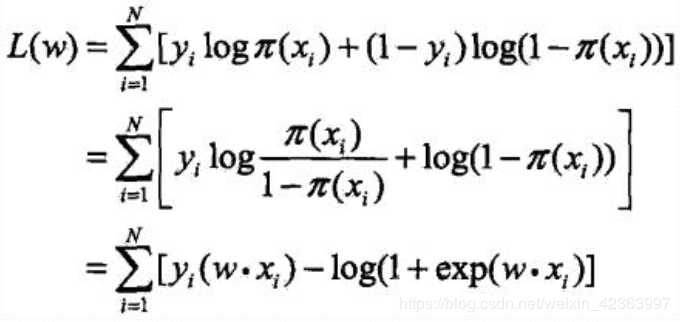
对L(w)求极大值， 得到w的估计值。
通常采用梯度下降法及拟牛顿法， 学到的模型：
4.多项logistic回归
设Y的取值集合为
多项logistic回归模型
原文：https://www.cnblogs.com/xutianlun/p/12248088.html