DFS。比较巧的一点是,利用 map <int , int> = line 存储。比如一号线上有两个相邻的站点 pre,end,那么就可以这样存储 map[pre*10000 + end] = map[end*10000 + pre] = 1,表示从 pre 到 end 和 end 到 pre 走的地铁线路是 1 号线。然后直接 dfs 就可以了,站点少的优先,若站点数相同,则换乘次数少的优先。
这道题让我又更加理解了最短路算法。我拿 DFS方法 做完之后,尝试着用最短路算法做。本以为会比较顺利,事与愿违 ??,虽然魔改代码后过了这道题,但是最短路算法对于这道题来说是不对的(然而我并不知道我想的对不对)。
题目中提到秉着第一:站数少的优先,第二:换乘次数少的优先的原则,使得路径唯一。数据确实保证了最终路径唯一,但是在用最短路算法求解的过程中中间路径不唯一的话,怎么办?(即最终路径唯一,中间路径不唯一)
举个栗子
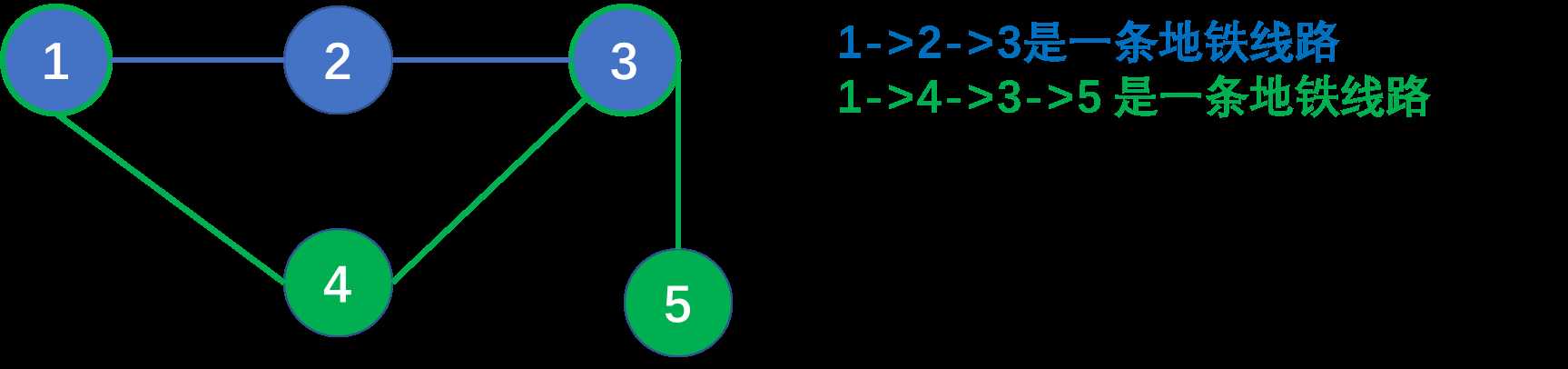
可以看出1 -> 5 的最优路径为1 -> 4 -> 3 -> 5(四站,零换乘)。
但是1 -> 5的中间路径1 -> 3 的最优路径却并不唯一。
1 -> 3 的最优路径为 1 -> 2 -> 3 或 1 -> 4 -> 3(三站,零换乘)。
因为常规的最短路算法中,只能存储一条路径,那么使用什么方法让它绝对更新像 1 -> 4 -> 3 这样的路径,而不是 1 -> 2 -> 3 这样的路径。
我百度到这道题目近 13 页的的题解。其中极大多数用了DFS这种方法,只有几篇博客采用了最短路算法。试了试上述这个例子,都过不去。
琢磨了一天的时间,我对这种情况有了些自己的理解。
最短路算法求解时,当执行更新属性时(如距离,耗时等),只跟 from , to 有关(即从哪来,到哪去),即局部最优可以得出整体最优。
但是这个题不只跟 from , to有关,还跟整条路径有关,即局部最优不能推出整体最优。
那么如何利用最短路算法求解这种中间路径不唯一的题呢(不要问我为什么非要拿最短路求解)?
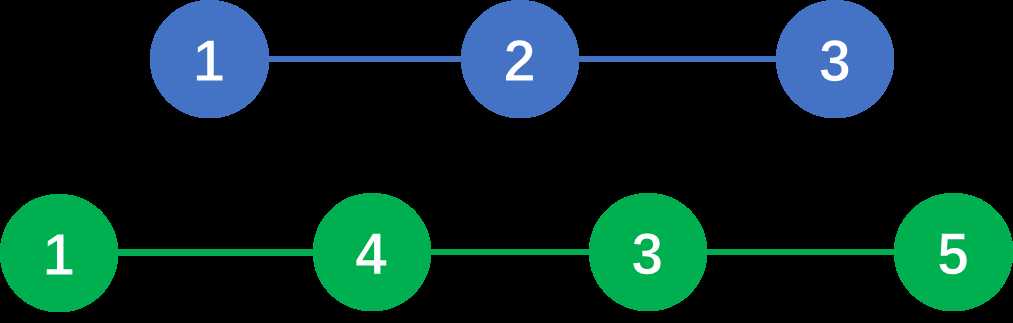
如上图,虽然有两个 1 和两个 3,但是他们都是同一个站点,代表着不同的状态。
就像 3 ,3 可以是换乘站(从一条地铁线到另一地铁线),也可以不是换乘站(在同一地铁线上)。
如何使用状态,去利用最短路算法求解呢?我不知道。
上述的这些可能是我的胡说八道,也可能是我菜的离谱不知道怎么利用最短路求解,也可能什么都不是。。??
?? 希望对这个问题有看法的 “同学” 可以评论我,救救孩子吧。??
??????这个是DFS的正确代码。
#include<bits/stdc++.h>
using namespace std;
const int inf=0x3fffffff;
map<int,int> imapi;
vector<int> edge[10005],path,tempath;
int S,D,vis[10005],mminsta,mmintrans;
void dfs(int p,int deep);
int check(vector<int> vec);
int main()
{
int i,j,n,k,pre,end,flag;
scanf("%d",&n);
for(i=1;i<=n;i++)
{
scanf("%d%d",&k,&pre);
for(j=1;j<k;j++)
{
scanf("%d",&end);
edge[pre].push_back(end);
edge[end].push_back(pre);
imapi[pre*10000+end]=imapi[end*10000+pre]=i;
pre=end;
}
}
scanf("%d",&n);
for(i=0;i<n;i++)
{
{
mminsta=mmintrans=inf;
fill(vis,vis+10005,0);
flag=-1;
}
scanf("%d%d",&S,&D);
tempath.push_back(S);
dfs(S,0);
tempath.pop_back();
printf("%d\n",mminsta);
for(j=1,pre=S;j<path.size();j++)
{
if(imapi[path[j-1]*10000+path[j]]!=flag)
{
if(flag!=-1)
{
printf("Take Line#%d from %04d to %04d.\n",flag,pre,end);
pre=end;
}
flag=imapi[path[j-1]*10000+path[j]];
}
end=path[j];
}
printf("Take Line#%d from %04d to %04d.\n",flag,pre,end);
}
system("pause");
return 0;
}
void dfs(int p,int deep)
{
int i;
if(p==D && (deep<mminsta||(deep==mminsta&&check(tempath)<mmintrans)))
{
mminsta=deep;
mmintrans=check(tempath);
path=tempath;
return ;
}
for(i=0;i<edge[p].size();i++)
{
if(vis[edge[p][i]]==0)
{
vis[edge[p][i]]=1;
tempath.push_back(edge[p][i]);
dfs(edge[p][i],deep+1);
vis[edge[p][i]]=0;
tempath.pop_back();
}
}
}
int check(vector<int> vec)
{
int i,flag=-1,cnt=0;
for(i=1;i<vec.size();i++)
{
if(imapi[vec[i-1]*10000+vec[i]]!=flag) cnt++;
flag=imapi[vec[i-1]*10000+vec[i]];
}
return cnt;
}
PAT (Advanced Level) 1131 Subway Map
原文:https://www.cnblogs.com/VividBinGo/p/12250885.html