概述
以监督学习为例,假设我们有训练样本集(x(i),y(i)),那么神经网络算法能够提供一种复杂且非线性的的假设模型hw,b(x),它具有参数W,b,可以以此参数来拟合我们的数据。
为了描述神经网络,我们先从最简单的神经网络讲起,这个神经网络仅由一个“神经元”构成,以下即是这个神经元的图示:
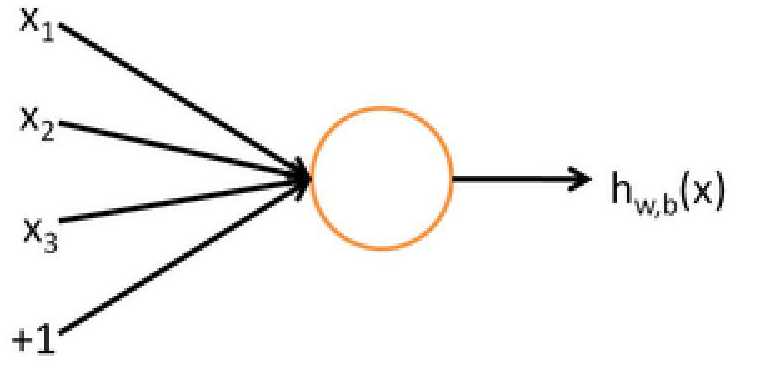
这个“神经元”是一个以x1,x2,x3及截距+1为输入值的运算单元,其输出为
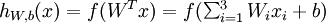
其中函数 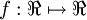 被称为“激活函数”。在本教程中,我们选择sigmoid函数作为激活函数f(.)
被称为“激活函数”。在本教程中,我们选择sigmoid函数作为激活函数f(.)
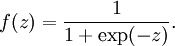
可以看出,这个单一“神经元”的输入——输出映射关系其实就是一个逻辑回归(logistic regression).
虽然本系列教程采用sigmoid函数,但你也可以选择双曲正切函数(tanh):
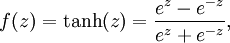
以下分别是sigmoid及tanh的函数图像
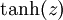 函数是sigmoid函数的一种变体,它的取值范围为
函数是sigmoid函数的一种变体,它的取值范围为 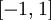 ,而不是sigmoid函数的
,而不是sigmoid函数的 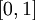 。
。
最后要说明的是,有一个等式我们以后会经常用到:如果选择 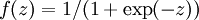 ,也就是sigmoid函数,那么它的导数就是
,也就是sigmoid函数,那么它的导数就是 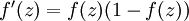 (如果选择tanh函数,那它的导数就是
(如果选择tanh函数,那它的导数就是 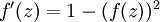 ,你可以根据sigmoid(或tanh)函数的定义自行推导这个等式。
,你可以根据sigmoid(或tanh)函数的定义自行推导这个等式。
神经网络模型
所谓神经网络就是将许多个单一“神经元”联结在一起,这样,一个“神经元”的输出就可以是另一个“神经元”的输入。例如,下图就是一个简单的神经网络:
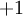 ”的圆圈被称为偏置节点,也就是截距项。神经网络最左边的一层叫做输入层,最右的一层叫做输出层(本例中,输出层只有一个节点)。中间所有节点组成的一层叫做隐藏层,因为我们不能在训练样本集中观测到它们的值。同时可以看到,以上神经网络的例子中有3个输入单元(偏置单元不计在内),3个隐藏单元及一个输出单元。
”的圆圈被称为偏置节点,也就是截距项。神经网络最左边的一层叫做输入层,最右的一层叫做输出层(本例中,输出层只有一个节点)。中间所有节点组成的一层叫做隐藏层,因为我们不能在训练样本集中观测到它们的值。同时可以看到,以上神经网络的例子中有3个输入单元(偏置单元不计在内),3个隐藏单元及一个输出单元。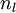 来表示网络的层数,本例中
来表示网络的层数,本例中 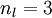 ,我们将第
,我们将第  层记为
层记为 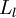 ,于是
,于是 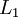 是输入层,输出层是
是输入层,输出层是 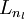 。
。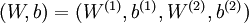 ,其中
,其中 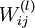 (下面的式子中用到)是第
(下面的式子中用到)是第  层第
层第  单元与第
单元与第 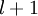 层第
层第  单元之间的联接参数(其实就是连接线上的权重,注意标号顺序),
单元之间的联接参数(其实就是连接线上的权重,注意标号顺序), 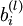 是第
是第 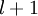 层第
层第  单元的偏置项。因此在本例中,
单元的偏置项。因此在本例中, 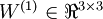 ,
, 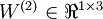 。
。 注意:没有其他单元连向偏置单元(即偏置单元没有输入),因为它们总是输出+1.同时。同时,我们用 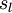 表示第
表示第  层的节点数(偏置单元不计在内)。
层的节点数(偏置单元不计在内)。
我们用 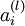 表示第
表示第  层第
层第  单元的激活值(输出值)。当
单元的激活值(输出值)。当 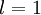 时,
时, 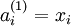 ,也就是第
,也就是第  个输入值(输入值的第
个输入值(输入值的第  个特征)。对于给定参数集合
个特征)。对于给定参数集合 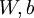 ,我们的神经网络就可以按照函数
,我们的神经网络就可以按照函数 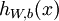 来计算输出结果。本例神经网络的计算步骤如下:
来计算输出结果。本例神经网络的计算步骤如下:
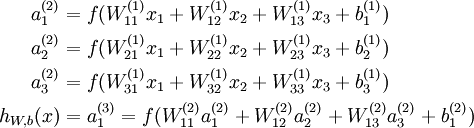
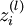 表示第
表示第  层第
层第  单元输入加权和(包括偏置单元),比如,
单元输入加权和(包括偏置单元),比如, 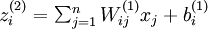 ,则
,则 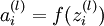 。 。
。 。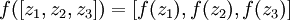 ,那么,上面的等式可以更简洁地表示为:
,那么,上面的等式可以更简洁地表示为: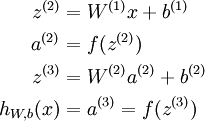
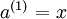 表示输入层的激活值,那么给定第
表示输入层的激活值,那么给定第  层的激活值
层的激活值 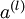 后,第
后,第 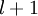 层的激活值
层的激活值 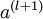 就可以按照下面步骤计算得到:
就可以按照下面步骤计算得到:
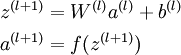
将参数矩阵化,使用矩阵-向量运算方式,我们就可以利用线性代数的优势对神经网络进行快速求解。
目前为止,我们讨论了一种神经网络,我们也可以构建另一种结构的神经网络(这里结构指的是神经元之间的联结模式),也就是包含多个隐藏层的神经网络。最常见的一个例子是 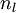 层的神经网络,第
层的神经网络,第 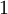 层是输入层,第
层是输入层,第 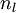 层是输出层,中间的每个层
层是输出层,中间的每个层  与层
与层 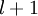 紧密相联。这种模式下,要计算神经网络的输出结果,我们可以按照之前描述的等式,按部就班,进行前向传播,逐一计算第
紧密相联。这种模式下,要计算神经网络的输出结果,我们可以按照之前描述的等式,按部就班,进行前向传播,逐一计算第 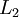 层的所有激活值,然后是第
层的所有激活值,然后是第 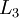 层的激活值,以此类推,直到第
层的激活值,以此类推,直到第 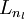 层。这是一个前馈神经网络的例子,因为这种联接图没有闭环或回路。
层。这是一个前馈神经网络的例子,因为这种联接图没有闭环或回路。
神经网络也可以有多个输出单元。比如,下面的神经网络有两个隐藏层: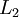 及
及 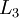 ,输出层
,输出层 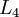 有两个输出单元。
有两个输出单元。
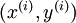 ,其中
,其中 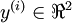 。如果你想预测的输出是多个的,那这种神经网络很适用。(比如,在医疗诊断应用中,患者的体征指标就可以作为向量的输入值,而不同的输出值
。如果你想预测的输出是多个的,那这种神经网络很适用。(比如,在医疗诊断应用中,患者的体征指标就可以作为向量的输入值,而不同的输出值 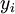 可以表示不同的疾病存在与否。)
可以表示不同的疾病存在与否。)原文:http://www.cnblogs.com/rong86/p/3518140.html