链接:https://zhuanlan.zhihu.com/p/74938375

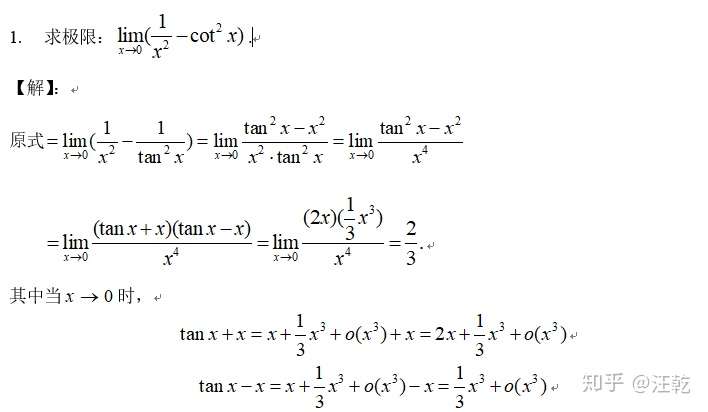
这里看似使用的等价无穷小,其实并不是这个样子的。是我们在使用了泰勒公式之后,才发现两者的结果一样。这里的分子和分母中最低阶的指数必须是一致的,也就是相同的强调过多次了。这也是我们泰勒公式使用时候的一个辅助信息,大家要牢牢把握。
泰勒公式在求极限问题中的本质就是帮助发现极限式中的因子的最低阶元素,也就是最有效的元素。我们使用泰勒公式就是要精准的定位到最有效的低阶元素。
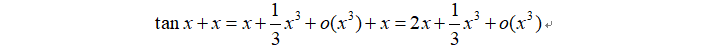
我们通过泰勒展开后得到的结果发现最低阶元素就是我们的一次方,故显然最后结果表现出来的就是类似于等价无穷小作出来的结果。
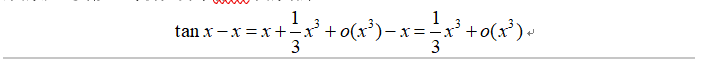
这个通过泰勒展开后,我们发现最低阶的一次方刚好被消去了,我们现在判断第二小的阶数是什么,发现是3次方。故得到以上结果。
2.1.2泰勒公式确定参数与无穷小阶数
①极限中确定参数的问题,通常使用泰勒公式求解最为快捷。
②确定无穷小的阶数,一定是泰勒公式处理



 2.1.3.泰勒公式误区
2.1.3.泰勒公式误区
①等价无穷小是粗略版本的泰勒公式,如何正确使用等价无穷小,加减法能用等价否???
②复合泰勒公式的使用.

这里大家可看出来了,首先使用等价无穷小其实在【正解】中的使用就不可取,因为不满足我们要求的精度,必须使用泰勒公式!
【错解2】:

这里为何又可以呢?
做一个系统的说明:我们在求极限的过程中,一定要注意到一点,我们“含有极限因子的因式”同剩下的“含有极限因子的因式整体”(常数不用管,比如第一题的底数为e,只有指数部分才有含极限因子的因式)为乘除关系,且其取极限之后的结果是一个“非零常数”,我们通常可以直接将其求出极限;如果我们对某个因式求了极限发现还含有极限因子,我们此时是不能够进行计算部分因式的极限的!







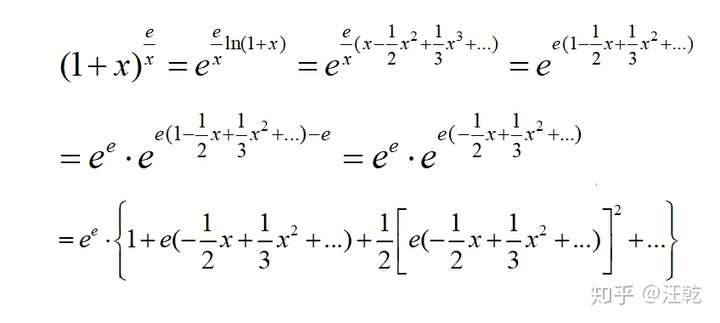



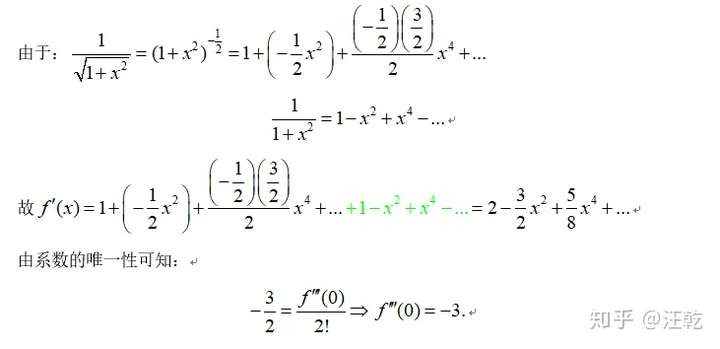
2.3泰勒中值定理
中值定理问题中涉及到二阶及其以上导数时,注意泰勒中值定理的使用



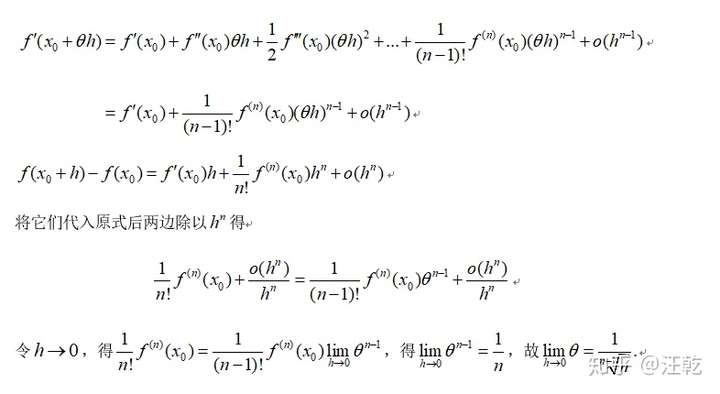
原文:https://www.cnblogs.com/Hqx-curiosity/p/12254637.html