当把函数与导数二者放置到一起时,许多高三学生都有点发懵,往往弄不清楚二者的关系,在我看来,函数应该是主题的核心内容,而导数仅仅是解决函数问题的一个工具,甚至都谈不上是唯一的工具,只是有些形式复杂的函数,为了研究其图像和性质,才不得不请出来的一个终极大法,对于比较简单的函数,我们往往采用杀鸡不用牛刀的策略来处理,以下举例作以说明。
【法1】:数形结合法[不完全分离参数法],由于函数\(f(x)\)的定义域为\((0,+\infty)\),
我们将函数有两个零点的问题转化为方程\(kx^2=lnx\)有两个不同的实数根的问题,
再次转化为函数\(y=kx^2\)与函数\(y=lnx\)的图像有两个不同的交点,
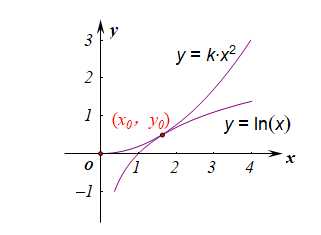
如图设两个函数的图像相切于点为\((x_0,y_0)\),
则有关系式\(\begin{cases}2kx_0=\cfrac{1}{x_0}\\kx_0^2=y_0\\y_0=lnx_0\end{cases}\),
解得\(y_0=\cfrac{1}{2},x_0=\sqrt{e}\),即切点为\((\sqrt{e},\cfrac{1}{2})\),
再代入函数\(y=kx^2\),求得此时的\(k=\cfrac{1}{2e}\),
再结合函数\(y=kx^2\)的系数\(k\)的作用,可得两个函数要有两个不同的交点,
则\(k\in(0,\cfrac{1}{2e})\)。 故选\(D\).
【法2】:完全分离参数法,定义域为\((0,+\infty)\),转化为方程\(kx^2=lnx\)有两个不同的实数根,
再转化为\(k=\cfrac{lnx}{x^2}\)有两个不同的实数根,
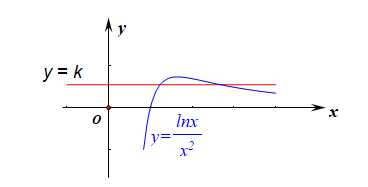
再转化为函数\(y=k\)和函数\(g(x)=\cfrac{lnx}{x^2}\)的图像有两个不同的交点,
用导数研究函数\(g(x)\)的单调性,\(g'(x)=\cfrac{\cfrac{1}{x}\cdot x^2-lnx\cdot 2x}{(x^2)^2}=\cfrac{1-2lnx}{x^3}\),
令\(1-2lnx>0\),得到\(0< x<\sqrt{e}\),令\(1-2lnx<0\),得到\(x >\sqrt{e}\),
即函数\(g(x)\)在区间\((0,\sqrt{e}]\)上单调递增,在\([\sqrt{e},+\infty)\)上单调递减,
故\(g(x)_{max}=g(\sqrt{e})=\cfrac{1}{2e}\),
作出函数\(g(x)\)和函数\(y=k\)的简图,由图像可得\(k\)的取值范围是\(k\in(0,\cfrac{1}{2e})\)。 故选\(D\).
解后反思:解法一可以认为是没有用导数的思路,只是在处理曲线和曲线相切时的切线时才不得不用导数这个工具。解法二大大方方的采用了导数,为什么要用导数呢,不用导数工具要研究新产生的函数\(g(x)\)的图像和性质,只能是瞎蒙,二者相比较,我们也就能清楚定位导数的工具地位了,它是为了研究更复杂形式的函数性质而生的。
原文:https://www.cnblogs.com/wanghai0666/p/12256266.html