http://poj.org/problem?id=1741
给一个有N个节点的树,每条边都有一个长度。两个节点之间的路径长度就是树上最短路径长度。问长度不超过k的路径一共有多少条。
$N\leqslant 10000$
树上分治,以p为根的树中路径有两种
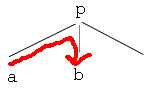
从一个子树沿着向上,然后朝下进入另外一个子树
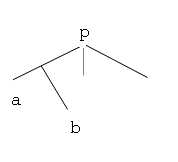
在p的同一个子树里面
可以看出来,第二种情况仍然会经过一个根
所以考虑第一种情况,然后递归考虑其他根的情况(转化为情况1)就可以了。
题目要求路径长度不超过k,不能直接枚举(时间复杂度$n^2\times n$,远远超过$10^9$),但是可以在遍历子树的时候寻找其他子树中剩余长度不超过$k-s$的节点数(不好写)
还可以把节点排序,类似于双指针,当l增大时,r一定不会增大,并且保证$l<r$,同时统计l到r中剩余的每个子树节点的个数
时间复杂度$\mathcal{O}(R\times (n \times \log n+n))$,如果只有一条链,那么$R=\mathcal{O}(n)$,仍然会超时,因此需要每次递归都选择重心作为根,那么$R=\mathcal{O}(\log n)$
时间复杂度$\mathcal{O}(n\times \log^2 n)$
代码能力下降……又写了一下午
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define REP(i,a,b) for(register int i=(a); i<(b); i++)
#define REPE(i,a,b) for(register int i=(a); i<=(b); i++)
using namespace std;
#define MAXN 10007
int n,k;
int vis[MAXN];
int sz[MAXN];
int hd[MAXN], to[MAXN<<1], nxt[MAXN<<1], le[MAXN<<1], es;
inline void init() {
es=0; memset(vis,0,sizeof vis); memset(hd,-1,sizeof(hd));
memset(sz,0,sizeof sz);
}
inline void adde(int a, int b, int c) {
nxt[es]=hd[a];hd[a]=es;to[es]=b;le[es]=c;es++;
nxt[es]=hd[b];hd[b]=es;to[es]=a;le[es]=c;es++;
}
//FINDS///////////////////////////////////////////////////
int zd, hp, S;
void dfsm(int p) {
vis[p]=1;
int s=1, mp=0;
for(int i=hd[p]; ~i; i=nxt[i]) if((!(vis[to[i]]&1)) && (!(vis[to[i]]&4))) {
dfsm(to[i]);
s+=sz[to[i]], mp=max(mp,sz[to[i]]);
}
mp = max(mp,S-s);
if(mp<zd) {
zd=mp, hp=p;
}
sz[p]=s;
}
void finds(int p, int s) {
zd=0x7fffffff;
S=s;
dfsm(p);
}
//GO//////////////////////////////////////////////////////
struct node {
int l, b;
bool operator<(const node&r) const {
return l<r.l;
}
} que[MAXN]; int qn; int cnt[MAXN];
void go(int p, int b, int l) {
vis[p]=2;
que[qn++]=(node){l, b};
for(int i=hd[p]; ~i; i=nxt[i]) if((!(vis[to[i]]&2)) && (!(vis[to[i]]&4))){
go(to[i], b, l+le[i]);
}
}
//////////////////////////////////////////////////////////
int ans;
void calc(int p, int s) {
finds(p,s);
p=hp;
vis[p]=-1;
qn=0;
que[qn++]=(node){0,p};
for(int i=hd[p]; ~i; i=nxt[i]) if(!(vis[to[i]]&4)) {
go(to[i], to[i], le[i]);
}
memset(cnt,0,sizeof cnt);
REP(i,0,qn) {
cnt[que[i].b]++;
}
sort(que,que+qn);
int l=0, r=qn-1;
while(l<r) {
cnt[que[l].b]--;
while(l<r && que[l].l+que[r].l>k) {
cnt[que[r].b]--;
r--;
}
ans+=r-l-cnt[que[l].b];
l++;
}
for(int i=hd[p]; ~i; i=nxt[i]) if(!(vis[to[i]]&4)) {
calc(to[i], sz[to[i]]);
}
}
int main() {
while(~scanf("%d%d", &n, &k) && (n||k)) {
init(); ans=0;
REP(i,1,n) {
int a,b,c; scanf("%d%d%d", &a, &b, &c);
adde(a,b,c);
}
calc(1,n);
printf("%d\n", ans);
}
}
原文:https://www.cnblogs.com/sahdsg/p/12256858.html