04. 卷积神经网络

第四周 特殊应用

4.1 人脸识别

首先要区别人脸验证（face verification）和人脸识别（face recognition）。

人脸验证（1:1）：输入图片和姓名（ID），系统判断输入图片是否为其所声明的身份；

人脸识别（1:K）：系统拥有一个K人的数据库，输入图片，如果此人存在于数据库，系统输出对应的身份，否则输出“未识别”。

4.2 单样本学习

在人脸检测的实际应用中，数据库中往往只有每个人的一张照片，要通过这一张照片学会如何识别身份所面临的问题就是单样本学习（one-shot learning）。

解决方法是借助一个相似性函数|( d(img1, img2) \)，用于评估两张照片属于同一个人的概率，设定一个阈值进行判断：

\( \begin{cases} d(img1,img2) \le \tau,\quad \text{same} \\ d(img1,img2) > \tau ,\quad \text{different}  \end{cases} \)

要完成人脸识别，需要将输入与数据库中所有的照片进行比对。

4.3 & 4.4 & 4.5 Siamese网络

Simese网络的做法是训练一个神经网络，当输入一张图片时，网络输出一个n维向量，当作对图片的编码\( f(x^{(i)}) \)，这个编码网络应当满足：

• 如果\( x^{(i)}\)和\( x^{(j)} \)是同一个人，那么 \( \|f(x^{(i)}) - f(x^{(j)})\|^2 \) 应该很小；
• 如果\( x^{(i)} \)和\( x^{(j)} \)不是同一个人，那么 \( \|f(x^{(i)}) - f(x^{(j)})\|^2 \) 应该很大；

方法一：

为了达到上面的目的，我们可以设计一个新的损失函数——三元损失（Triplet Loss）。里面的三元分别是anchor, positive和negative，anchor表示基准图像，positive是与anchor属于同一个人的照片，negative是与anchor属于不同人的照片。

我们的想法是在训练的时候以这样的一个三元组为基础，尽量让anchor和positive之间的差距小于anchor和negative之间的距离，具体表达式如下：

\( L(A,P,N) = \max\left(\|f(A) - f(P)\|^2 - \|f(A) - f(N)\|^2 + \alpha, 0\right) \)

\( \begin{gathered} J = \sum_{i=1}^m L(A^{(i)}, P^{(i)}, N^{(i)}) \end{gathered} \)

其中的 \( \alpha \) 是一个超参数，类似于支持向量机中的间隔（margin），是为了让模型更robust。

在训练这个网络时要求我们的训练集中应该包含每一个人的多张照片，如1k个人的10k张照片。而在实际应用时就可以只依靠一张图片进行学习了。

方法二：

除了triplet loss，我们还可以将上面的“距离度量+阈值判断”问题合并为一个二分类问题，即输入两张照片，网络自己判断这两张图是否属于同一个人。

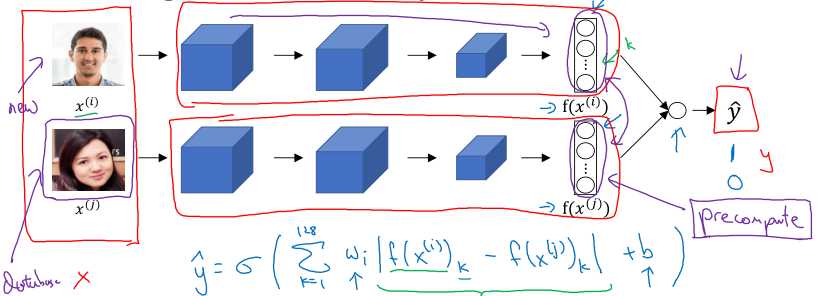
注意：

• 这里虽然看起来有两个网络，但其实这两路的参数是一样的，你必须确保提取特征的网络是同一个，否则将没有可比性；
• sigmoid函数的输入可以有多种选择，可以是两张照片的特征向量差值绝对值、可以是差值的平方等等；
• 在实际应用时，数据库中的照片可以预先计算好特征向量，与新照片的特征向量直接输入分类器进行判决；

4.6 风格迁移

啥是风格迁移？一张图说明：

4.7 深层卷积网络可视化

介绍一下卷积神经网络的可视化。我们经常看到一些说明卷积神经网络在干什么的文章使用类似下面的图像：

这种图是怎么得到的呢？其实它不是把卷积神经网络的各层feature转换成图片进行显示。

以上图为例，在网络其中一层的一个神经元（在卷积网络中就是一个卷积核的卷积输出）中寻找激活值较大的位置点，显然这一层的每个点对应着上一层的一块区域（计算卷积的区域），最终对应着原始图片中的一块图案。把这些对应激活值较大的图案裁剪出来就得到上面的图了。上面的图在每一层选了9个神经元，每个神经元上选择9个激活值较大的点，显然层数越深感受野越大，对应输入图片中的区域就越大。

4.8 & 4.9 & 4.10 风格迁移的代价函数

首先说明一下如何得到生成的图像：

1. 随机初始化一幅图像\( G \)；
2. 用梯度下降最小化\( J(G) = \alpha J_{\text{content}}(C,G) + \beta J_{\text{style}}(S,G) \)

下面分别介绍一下内容代价函数（content cost function）和风格代价函数（style cost function）。

内容代价函数

前面进行卷积网络的中间可视化时发现，中间层的特征包含着图像的内容，有了这种认识，就往下看。

使用预训练模型（如VGG），取隐藏层 \( l \) 计算内容代价，用\( a^{[l](C)} \)和\( a^{[l](G)} \)表示图像在\(l\)层的激活值：

\( J_{\text{content}}(C,G) = \| a^{[l](C)} - a^{[l](G)} \|^2 \)

风格代价函数

首先要定义什么是图像的风格（style）。前面讲卷积网络中间一层的各个神经元（对应不同通道）关注的内容都不一样，有的神经元可能关注图像中的一些条纹，有的神经元可能关注图像中的一些色块，而这些内容之间的对应关系就是风格。比如，有条纹的地方可能同时也有特殊的色块等等。而这一点可以通过计算通道之间的相关性来得到。

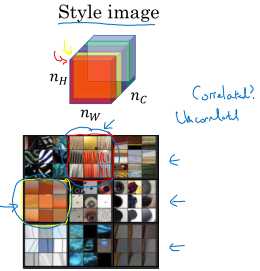
所以图像的风格表述为：激活值通道间的相关性。

\( \begin{gathered} G_{kk‘}^{[l](S)} = \sum_{i=1}^{n^{[l]}_H} \sum_{j=1}^{n^{[l]}_W} a^{[l](S)}_{ijk} a^{[l](S)}_{ijk‘} \end{gathered} \)

\( \begin{gathered} G_{kk‘}^{[l](G)} = \sum_{i=1}^{n^{[l]}_H} \sum_{j=1}^{n^{[l]}_W} a^{[l](G)}_{ijk} a^{[l](G)}_{ijk‘} \end{gathered} \)

\( \begin{gathered} J_{\text{style}^{[l]}}(S,G) =  \frac{1}{(2n_H^{[l]} n_W^{[l]} n_C^{[l]})^2} \sum_k \sum_{k‘} (G_{kk‘}^{[l](S)} - G_{kk‘}^{[l](G)})^2 \end{gathered}  \)

这种相关性是以\( n^{[l]}_G \times n^{[l]}_C \)风格矩阵\(G\)的形式来表示。

计算所有层的风格损失会让效果更好，同时加上权重：

\( \begin{gathered} J_{\text{style}}(S,G) = \sum_l \lambda^{[l]} J_{\text{style}}^{[l]}(S,G) \end{gathered} \)

4.11 模型在1D和3D数据上的通用性

卷积的方法同样可以拓展到1D和3D数据上：

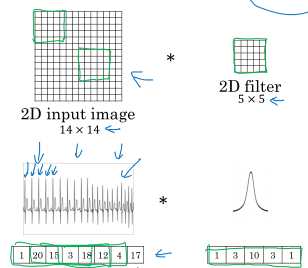
你可能觉得3D好像和原来的2D卷积没有区别，但真正的3D卷积中，第三个维度并不表示通道，像上图这样的立方体等同于于卷积网络中\( H \times W \times 1 \)的数据。

吴恩达深度学习课程笔记-12

原文：https://www.cnblogs.com/tofengz/p/12257137.html