一个无向图G的最小生成树是由该图的那些连接G的所有顶点的边构成的树,且其总价值(边的权值的和)最低。
用Prim算法实现最小生成树
先把图看作许多个零散的顶点,顶点之间无联系,然后选一个作为树的开始顶点。算法的每一阶段都通过选择边(u,v),使得(u,v)的值是所有u在树上但v不在树上的边中的最小者,找出这样一个新的顶点并把它添加到这棵树上。
代码如下:
1 #include <iostream> 2 3 using namespace std; 4 #define MAX_VERTEX_NUM 10//最大顶点个数 5 #define INF 32768 6 7 //邻接表 8 struct ENode//边结点 9 { 10 int index;//边所指向的点的序号 11 int info;//记录权值 12 struct ENode* next;//指向下一条边 13 }; 14 struct VNode//顶点结点 15 { 16 char data;//顶点名称 17 ENode* first;//指向顶点的第一个邻边 18 }; 19 struct AGraph//记录图的信息 20 { 21 int vexnum, arcnum;//顶点数和边数 22 VNode p[MAX_VERTEX_NUM];//顶点数组 23 }; 24 25 int LocateVex(AGraph *G, char ch) 26 { 27 for (int i = 0; i < G->vexnum; i++) 28 if (ch == G->p[i].data) 29 { 30 return i; 31 break; 32 } 33 return -1; 34 } 35 //创建邻接表 36 void CreateAGraph(AGraph *G) 37 { 38 int i, j, info; 39 char v1, v2; 40 cout << "请输入顶点个数:" << endl; cin >> G->vexnum; 41 cout << "请输入边的个数:" << endl; cin >> G->arcnum; 42 cout << "构造顶点:" << endl; 43 for (int i = 0; i < G->vexnum; i++)//构造顶点数组 44 { 45 cin >> G->p[i].data; 46 G->p[i].first = NULL; 47 } 48 cout << "构造邻接表:" << endl; 49 for (int k = 0; k < G->arcnum; k++)//无向图 50 { 51 cin >> v1 >> v2 >> info; 52 i = LocateVex(G, v1); 53 j = LocateVex(G, v2); 54 ENode *E = (ENode*)malloc(sizeof(ENode)); 55 E->index = j;//边(i,j) 56 E->info = info; 57 E->next = G->p[i].first;//头插法 58 G->p[i].first = E; 59 ENode *E1 = (ENode*)malloc(sizeof(ENode)); 60 E1->index = i;//边(j,i) 61 E1->info = info; 62 E1->next = G->p[j].first; 63 G->p[j].first = E1; 64 } 65 } 66 // 67 struct TableNode 68 { 69 int known;//顶点是否已处理 70 int dist;//距离 71 char path;//记录该顶点的前驱顶点 72 }; 73 typedef TableNode Table[MAX_VERTEX_NUM]; 74 //初始化Prim算法中使用的表 75 void CreateTable(Table T,int start)//start为起始的顶点 76 { 77 for (int i = 0; i < MAX_VERTEX_NUM; i++) 78 { 79 T[i].known = 0;//顶点未处理 80 T[i].dist = INF;//距离为INF 81 T[i].path = 0;//表示前面没接顶点 82 } 83 T[start].dist = 0; 84 } 85 //Prim算法 86 void Prim(AGraph* G, Table T,int start) 87 { 88 int minindex = start; 89 int count = 0;//记录已标记的顶点个数 90 while (count != G->vexnum)//还有顶点未处理 91 { 92 int mindist=INF; 93 int v=minindex; 94 T[v].known = 1; 95 count++; 96 //对相邻顶点进行调整 97 if (G->p[v].first != NULL) 98 { 99 ENode* e = G->p[v].first; 100 while (e) 101 { 102 if (T[e->index].known == 0 && T[e->index].dist > e->info) 103 { 104 T[e->index].dist = e->info; 105 T[e->index].path = G->p[v].data; 106 } 107 e = e->next; 108 } 109 } 110 //找出表中dist最小且未处理过的顶点的编号minindex,将其入队 111 for (int i = 0; i<G->vexnum; i++) 112 if(T[i].known == 0) 113 if (T[i].dist < mindist) 114 { 115 minindex = i; 116 mindist = T[i].dist; 117 } 118 } 119 } 120 //打印表 121 void PrintTable(AGraph* G,Table T) 122 { 123 cout << "执行Prim后的Table:" << endl; 124 for (int i = 0; i < G->vexnum; i++) 125 cout << T[i].known << " " << T[i].dist << " " << T[i].path << endl; 126 } 127 int main() 128 { 129 int start = 0; 130 AGraph* G = (AGraph*)malloc(sizeof(AGraph)); 131 CreateAGraph(G); 132 Table T; 133 CreateTable(T, start); 134 Prim(G, T, start); 135 PrintTable(G, T); 136 system("pause"); 137 return 0; 138 }
创建的无向图和其最小生成树如下:
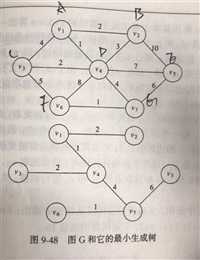
运行结果:

原文:https://www.cnblogs.com/cs0915/p/12259172.html