给你n根火柴棍,你可以拼出多少个形如“A+B=CA+B=C”的等式?等式中的AA、BB、CC是用火柴棍拼出的整数(若该数非零,则最高位不能是00)。用火柴棍拼数字0-90−9的拼法如图所示:

注意:
加号与等号各自需要两根火柴棍
如果A≠BA?=B,则A+B=CA+B=C与B+A=CB+A=C视为不同的等式(A,B,C>=0A,B,C>=0)
nn根火柴棍必须全部用上
一个整数n(n<=24)n(n<=24)。
一个整数,能拼成的不同等式的数目。
输入#1
| 14 |
输出#1
| 2 |
输入#2
| 18 |
输出#2
| 9 |
【输入输出样例1解释】
22个等式为0+1=10+1=1和1+0=11+0=1。
【输入输出样例2解释】
99个等式为:
0+4=4
0+11=11
1+10=11
2+2=4
2+7=9
4+0=4
7+2=9
10+1=11
11+0=11
#include<iostream> using namespace std; int a[10]={6,2,5,5,4,5,6,3,7,6}; //将每一个数字的对应所需的火柴数存入对应的数组中 int b[2001]={6}; //将数字为0的火柴数定义为6个,由于需要的数字可以组成最多三位数字,且符合条件n(所给火柴数)<=24 int main(){ int n; int count=0; cin>>n; for(int i=1;i<2001;i++){ //将每一个数字(包括10~2000)所对应的火柴数写入相应的数组中,例:b[10]=a[0]+a[1];而在前面完成了b[1]=a[1],b[2]=a[2],... ,所以b[j]=b[j]+a[j%10];j/=10;(j=i;) int j=i; while(j>=1){ b[i]+=a[j%10]; j/=10; } } for(int i=0;i<=1000;i++){ for(int j=0;j<=1000;j++){ if(b[i]+b[j]+b[i+j]==(n-4)){ //从0~2000中寻找符合这个条件的i和j,同时第三个数i+j也就确定下来了,满足就++ // cout<<i<<"+"<<j<<"="<<i+j<<endl; //这个是输出所有的满足条件的火柴棒等式 count++; } } } cout<<count; return 0; }
结果:
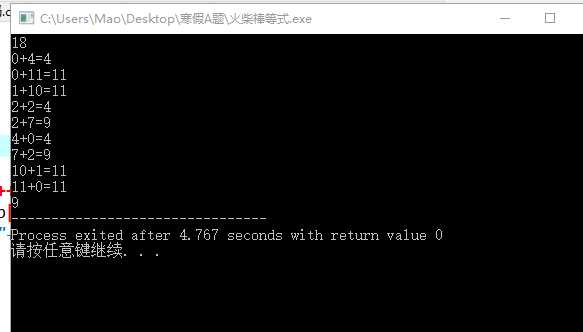
注意:洛谷中对于数组的要求很严格,这个数组中必须到2000,是因为这个可以到三位数进行加减,但是如果后面不进行定义,则会默认为0,也会使得火柴棒等式满足,所以到2000,是满足了n<=24的极限条件,同时会使等式符合;
原文:https://www.cnblogs.com/zmz-zero/p/12260740.html