进制的基本转换:
十进制、二进制互转
1)十进制转化成二进制,除以2取余数
2)二进制转化成十进制,乘以2的幂数
十进制、八进制互转
1)十进制转化成八进制,除以8取余数
2)八进制转化成十进制,乘以8的幂数
十进制、十六进制互转
1)十进制转化成十六进制,除以16取余数
2)16进制转化成十进制,乘以16的幂数
负数的二进制表现形式
对应的整数二进制取反加1
例子:
二进制转化为其他进制
1)二进制转化成十进制:
1011 = 1*2(0)+1*2(1)+0*2(2)+1*2(3)= 11
2)二进制转化成八进制(三个一分段):
010101110 = 010-----------------101------------------------- 110 = 0256
2=1*2(1) 5=1*2(0) +1*2(2) 6=1*2(1)+1*2(2)
3)二进制转化成十六进制(4个一分段):
10101110 = 1010 ------------------------------1110 = 0xAE
10=1*2(1)+1*2(3) 14=1*2(1)+1*2(2)+1*2(3)
10 11 12 13 14 15
A B C D E F
结论:
八进制数:其实就是二进制中的三个二进制位为一个八进制位
十六进制:其实就是二进制中的四个二进制位为一个十六进制位
十进制转化成其他进制
方法一:
1)十进制转化成二进制
6=110
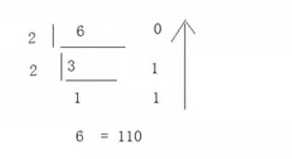
2)将转化成的二进制,转化成八进制或十六进制参考上方
方法二:
参考:https://mp.weixin.qq.com/s?src=11×tamp=1580911749&ver=2140&signature=h-gqu3GT-YG1BQdytJzof7Itqfk*s8AYilB5100km0LrcnOwMbl2weX-ekZ2DS3c88yVeOT*OKemJJsEPSKlmjkn*3vs2Mh7q4t8-URPAFy1Kmen0zJb4bxodfZ8iX16&new=1
将十进制转换为其它进制时比较复杂,整数部分和小数部分的算法不一样
1)整数部分:
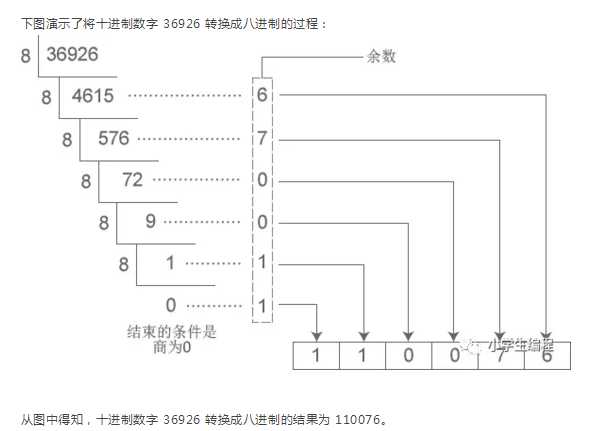
十进制整数转换为 N 进制整数采用“除 N 取余,逆序排列”法。具体做法是:
将 N 作为除数,用十进制整数除以 N,可以得到一个商和余数;
保留余数,用商继续除以 N,又得到一个新的商和余数;
仍然保留余数,用商继续除以 N,还会得到一个新的商和余数;
……
如此反复进行,每次都保留余数,用商接着除以 N,直到商为 0 时为止。
把先得到的余数作为 N 进制数的低位数字,后得到的余数作为 N 进制数的高位数字,依次排列起来,就得到了 N 进制数字。
十进制小数转换成 N 进制小数采用“乘 N 取整,顺序排列”法。具体做法是:
用 N 乘以十进制小数,可以得到一个积,这个积包含了整数部分和小数部分;
将积的整数部分取出,再用 N 乘以余下的小数部分,又得到一个新的积;
再将积的整数部分取出,继续用 N 乘以余下的小数部分;
……
如此反复进行,每次都取出整数部分,用 N 接着乘以小数部分,直到积中的小数部分为 0,或者达到所要求的精度为止。
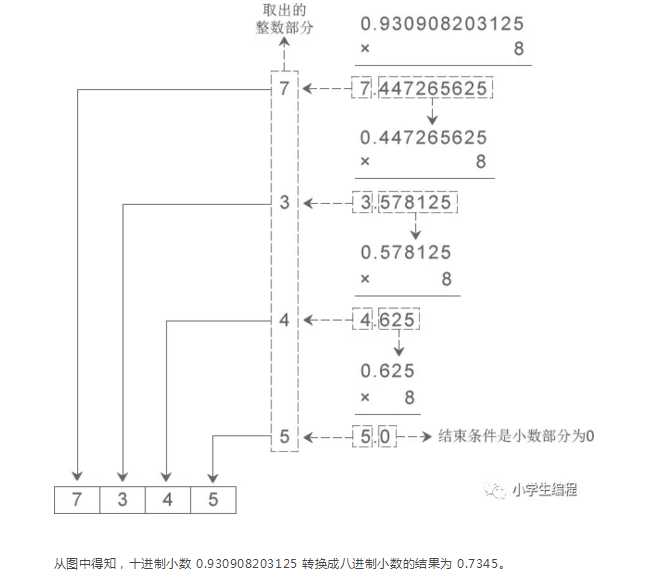
把取出的整数部分按顺序排列起来,先取出的整数作为 N 进制小数的高位数字,后取出的整数作为低位数字,这样就得到了 N 进制小数。
下图演示了将十进制小数 0.930908203125 转换成八进制小数的过程:
负数的二进制表现
负数的二进制最高位是1
原文:https://www.cnblogs.com/prince365/p/12266994.html