什么是二分图 ?
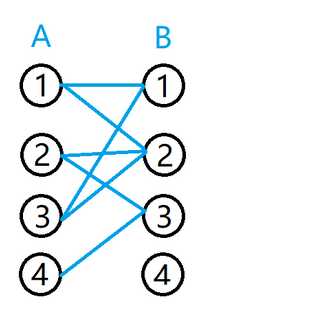
先介绍一下什么是二分图,二分图也叫二部图,设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图,如下图所有的顶点可以分成A,B两个集合,而A集合与B集合中的点与自己的阵营的点是没有连线的(A集合的点只与B集合的点有边相连),则称这个为一个二分图
定义 :
无向图G位二分图的一个充要条件是
1.G中至少包含两个顶点.
2.G中所有的回路必须长度必须是偶数
(即图中所形成的环路中的结点必须是偶数个!)。
附赠必备概念 :
1.匹配
设G = <V,E>为二分图,如果 M?E,并且 M 中两点没有任何两点有公共端点(被其他匹配的边共用),则成M为G的一个匹配。【也就是说匹配的实质是一些边的集合。】
2.最大匹配: 对于二分图G的一个子图M,若M为其边数最多的子图,
则称M为G的最大匹配。
原文:https://www.cnblogs.com/wlw-x/p/11563258.html