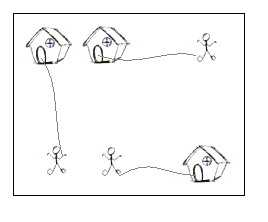
您可以将栅格地图上的每个点都视为一个很大的正方形,因此它可以同时容纳n个矮个子。 同样,如果一个小男人跨进带有房屋的网格而不进入该房屋也可以。
Input
Output
Sample Input
2 2
.m
H.
5 5
HH..m
.....
.....
.....
mm..H
7 8
...H....
...H....
...H....
mmmHmmmm
...H....
...H....
...H....
0 0
Sample Output
2
10
28
解题思路
对于此题,看起来十分复杂,没有思路,但是如果你了解二部图以及相关算法,这个题目可以直接套模板解决。我在网络上经过了仔细的查找,发现两篇不错的博文,使用了简单易懂的例子,讲的特别清晰,如下:
本题目需要用到的是KM算法,但是,其基础是匈牙利算法,所以,如果大家不理解匈牙利算法应该先看第一篇博文。
上文中,讲解KM算法的那篇博文里,用的是找对象的例子,匹配原则是好感度尽可能大,此题目的匹配原则是回家的花费尽可能少,所以需要在博文中给出的算法模板中稍作修改,即可使用。
修改的第一个地方:
// 每个女生的初始期望值是与她相连的男生最大的好感度 for (int i = 0; i < N; ++i) { ex_girl[i] = love[i][0]; for (int j = 1; j < N; ++j) { ex_girl[i] = max(ex_girl[i], love[i][j]); } } ------改为------ // 改为取最小值 for (int i = 0; i < N; ++i) { ex_girl[i] = love[i][0]; for (int j = 1; j < N; ++j) { ex_girl[i] = min(ex_girl[i], love[i][j]); } }
修改的第二个地方:
for (int j = 0; j < N; ++j) { // 所有访问过的女生降低期望值 if (vis_girl[j]) ex_girl[j] -= d; // 所有访问过的男生增加期望值 if (vis_boy[j]) ex_boy[j] += d; // 没有访问过的boy 因为girl们的期望值降低,距离得到女生倾心又进了一步! else slack[j] -= d; ------改为------ for (int j = 0; j < N; ++j) { // 改为增加 if (vis_girl[j]) ex_girl[j] += d; // 所有访问过的减少 if (vis_boy[j]) ex_boy[j] -= d; // 没有访问过的增加 else slack[j] += d;
经过以上两个地方的i修改,就成了求解最小期望和的模板,与此题目相适应,套一下模板即可。源代码戳下面链接即可,有完整注释~
源代码
C++ 11新标准实现POJ No.2195-GoingHome
原文:https://www.cnblogs.com/WongWai95/p/POJ-2195--WITH-CPP-11.html