首先开头说一下花了我半个小时debug的一个很弱智的错误!!:
错误:for(p=G->list[v].firstarc; p; p->next);
正解:for(p=G->list[v].firstarc; p; p=p->next);
??佛了
p忘记指向下一个指针,然后这里就无限循环
下面开始学习的Dijkstra算法:
此算法不可处理负数路径,即,如果有一条边权值为负数,那么Dijkstra算法无法处理。
以下为算法思路:(设原点为s)
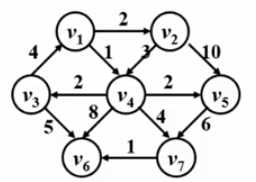 根据此图,假设原点为v1
根据此图,假设原点为v1
1.新建一个数组int collected[n],代表n下标的结点是否访问过次结点,1为访问过,0为未访问,初始化数组为0;
2.新建一个数组int dist[n],代表n下标的结点与原点的距离;初始化为正无穷;
3.新建一个数组int path[n],代表到达n下标节点所经过的前一个结点;初始化为-1;
最初状态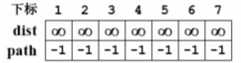
4.首先将原点dist[s]=0,path[s]=-1;原点到原点无距离;并且将原点collected[s]=1,代表访问过;
5.与原点最开始相连的几个节点开始遍历dist设置为原点到结点的权重,并将之path设置为s
dist[s] = 0; collected[s] = 1; for (p = G->list[s].firstarc; p; p = p->next) { dist[p->adjvex] = p->wei; //adjvex为节点下标,wei为权值 if (dist[p->adjvex] < INFINITY) //若之间的权值小于正无穷, path[p->adjvex] = s; //则路径下标置为原点 }
6.下面一步为正式算法
while (1) { w = FindMinDist(G, dist, collected); //此处这个FindMinDist为找出(未访问过的节点当中dist最小的结点)的下标,函数在下面 if (w == -1) //此处假设-1为节点不存在,跳出循环 break; collected[w] = 1; //首先将该节点置为1代表访问 for (p = G->list[w].firstarc; p; p = p->next) //该节点从第一个边遍历 { if (collected[p->adjvex] == 0 && p->wei < INFINITY) //判断:若边的结点未访问过且不为无穷大 { if (dist[w] + p->wei < dist[p->adjvex]) //判断原点到下标为w的结点距离+这条边权值,是否小于原点直接到这个结点的距离 { dist[p->adjvex] = dist[w] + p->wei; //如果是,原点到这条边的距离设置为下标为w的结点距离+这条边的权值 path[p->adjvex] = w; //路径设置为刚经过的w } } } }
【找出未访问过的节点当中,dist最小的结点的下标】算法:
int FindMinDist(Graph *G, int dist[], int collected[]) { int MinV, V; int MinDist = INFINITY; for (V = 1; V <= G->Vertexnum; V++) { if (collected[V] == 0 && dist[V] < MinDist) { /* 若V未被访问过,且dist[V]更小 */ MinDist = dist[V]; /* 更新最小距离 */ MinV = V; /* 更新对应顶点 */ } } if (MinDist < INFINITY) /* 若找到最小dist */ return MinV; /* 返回对应的顶点下标 */ else return -1; /* 设返回-1为不存在 */ }
以下为图解,更为直观
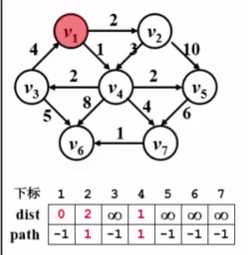
2. 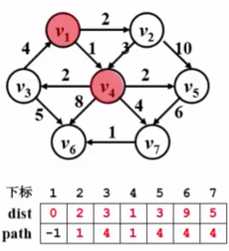
接着,找到未访问过的结点中v4最小了,所以,进行上一步循环,设置v4已访问,与之相连的有v3,v6,v7,v5.
先看v3:根据上一步,dist[3]为∞,而dist[4]+(v4到v3的权值)=3,显然小于dist[3],所以令dist[3]=dist[4]+(v4到v3的权值),并且将path[3]=4;
同理v6,v7,v5方法相同,完成后如上图。
3.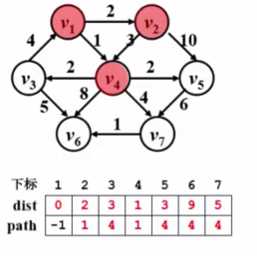
v1,v4已访问,未访问的中dist最小的就是v2了,
如上同理,但是其中有一点v2到v5权值为10,10+2明显大于3,所以不管它
4.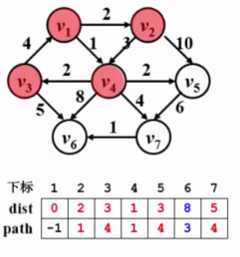
继续下一步,方法同上,注意到dist[3]+5=8 小于dist[6]的9。所以更新dist[6]=8,更新path[6]=3
5.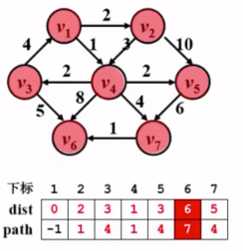
最终如上图,dist[7]+1=6,小于原来的dist[6]=8
所以dist[6]=6;path[6]=7;
6.然后,因为所有点均已访问,所以跳出循环,Dijkstra算法完成,已找到原点到所有点的最小路径。
若要输出某个节点到原点的路径:
因为输出路径事反着的,所以要用到栈 假设从原点到下标为u的节点 struct Stack{ int top = -1; int data[MAX]; }; Stack sq; sq.data[++sq.top] = u; //首元素压入栈 while (u != -1){ //若u=-1,说明已经到了原点,跳出循环 sq.data[++sq.top] = path[u]; //将下一个路径压入栈 u= path[u]; //使得u等于次结点的上一个路径 } while (sq.top != -1){ //依次出栈,即为路径 cout << G->list[sq.data[--sq.top]].name << ","; }
还是以此图为例题程序:
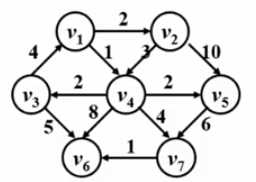

#include <iostream> #include <fstream> #define MAX 50 #define INFINITY 114514 //此数为正无穷大,可以随便设置,如32767等等 using namespace std; ofstream out("H:/vscode/out.txt"); ifstream in("H:/vscode/in.txt"); int dist[MAX]; //原点到下标对应的顶点距离 int path[MAX]; //经过的路径 int collected[MAX]; //访问过的结点 typedef struct Arc { int adjvex; Arc *next; int wei; } Arc; struct Vertex { string name; Arc *firstarc; }; struct Graph { int Arcnum; int Vertexnum; Vertex list[MAX]; }; Graph *CreateGraph(int Vn, int An) //Vn 顶点数 ,An 边数 { Graph *G = new Graph; G->Vertexnum = Vn; G->Arcnum = An; for (int k = 1; k <= Vn; k++) { in >> G->list[k].name; G->list[k].firstarc = NULL; } return G; } void InsertArc(Graph *&G, int V1, int V2, int weight) { Arc *p = new Arc; p->adjvex = V2; p->wei = weight; p->next = G->list[V1].firstarc; G->list[V1].firstarc = p; } void outputGraph(Graph *G) { for (int i = 1; i <= G->Vertexnum; i++) { Arc *p; out << G->list[i].name << ": "; for (p = G->list[i].firstarc; p; p = p->next) { out << "(" << G->list[p->adjvex].name << "," << p->wei << ") "; } out << endl; } } void buildPath(Graph *&G) { int V1, V2, weight; for (int i = 1; i <= G->Arcnum; i++) { in >> V1 >> V2 >> weight; InsertArc(G, V1, V2, weight); } } int FindMinDist(Graph *G, int dist[], int collected[]) { /* 返回未被收录顶点中dist最小者 */ int MinV, V; int MinDist = INFINITY; for (V = 1; V <= G->Vertexnum; V++) { if (collected[V] == false && dist[V] < MinDist) { /* 若V未被收录,且dist[V]更小 */ MinDist = dist[V]; /* 更新最小距离 */ MinV = V; /* 更新对应顶点 */ } } if (MinDist < INFINITY) /* 若找到最小dist */ return MinV; /* 返回对应的顶点下标 */ else return -1; /* 若这样的顶点不存在,返回错误标记 */ } void Dijkstra(Graph *G, int v) //v为原点 { struct Stack { int top = -1; int data[MAX]; }; for (int i = 1; i <= G->Vertexnum; i++) { path[i] = -1; dist[i] = INFINITY; collected[i] = 0; } Arc *p; int w; dist[v] = 0; collected[v] = 1; for (p = G->list[v].firstarc; p; p = p->next) { dist[p->adjvex] = p->wei; if (dist[p->adjvex] < INFINITY) path[p->adjvex] = v; } while (1) { w = FindMinDist(G, dist, collected); if (w == -1) break; collected[w] = 1; for (p = G->list[w].firstarc; p; p = p->next) { if (collected[p->adjvex] == 0 && p->wei < INFINITY) { if (dist[w] + p->wei < dist[p->adjvex]) { dist[p->adjvex] = dist[w] + p->wei; path[p->adjvex] = w; } } } } for (int i = 1; i <= G->Vertexnum; i++)//输出从原点到所有点的最短路径 { Stack sq; out <<"from "<<G->list[v].name << " to " << G->list[i].name << " need " << dist[i] << endl; int j = i; sq.data[++sq.top] = j; while (j != -1) { sq.data[++sq.top] = path[j]; j = path[j]; } while (sq.top != -1) { out << G->list[sq.data[--sq.top]].name << " "; } out << endl; } } int main() { int Vn, An; //定点数和边数 in >> Vn >> An; Graph *G = CreateGraph(Vn, An); buildPath(G); outputGraph(G); Dijkstra(G, 3);//假设从原点为3,开始 system("pause"); }
以下in.txt
/*in.txt*/ 7 12 v1 v2 v3 v4 v5 v6 v7 0 1 2 0 3 1 1 3 3 1 4 10 2 0 4 2 5 5 3 2 2 3 4 2 3 5 8 3 6 4 4 6 6 6 5 1
以下out.txt
/*out.txt*/ v1: (v4,1) (v2,2) v2: (v5,10) (v4,3) v3: (v6,5) (v1,4) v4: (v7,4) (v6,8) (v5,2) (v3,2) v5: (v7,6) v6: v7: (v6,1) from v3 to v1 need 4 v3 v1 from v3 to v2 need 6 v3 v1 v2 from v3 to v3 need 0 v3 from v3 to v4 need 5 v3 v1 v4 from v3 to v5 need 7 v3 v1 v4 v5 from v3 to v6 need 5 v3 v6 from v3 to v7 need 9 v3 v1 v4 v7
原文:https://www.cnblogs.com/Itukas/p/12271761.html