10.1 图的定义和相关术语
图由顶点和边组成,每条边的两端都必须是图的两个顶点。而记号G(V,E)表示图G的顶点集为V、边集为E。
一般来说,图可分为有向图和无向图。有向图的所有边都有方向,即确定了顶点到顶点的一个指向;而无向图的所有边都是双向的,即无向边所连接的两个顶点可以互相到达。
10.2 图的存储
一般来说,图的存储方式有两种:邻接矩阵和邻接表。
10.2.1 邻接矩阵
令二维数组G[N][N]的两维分别表示图的顶点标号,即如果G[i][j]为1,则说明顶点i和顶点j之间有边;如果G[i][j]为0,则说明顶点i和顶点j之间不存在边,而这个二维数组G[][]则被称为邻接矩阵。
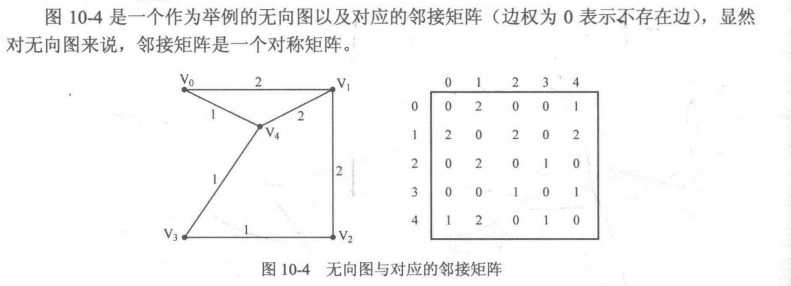
邻接矩阵只适用于顶点数目不太大(一般不超过1000)的题目。
10.2.2 邻接表
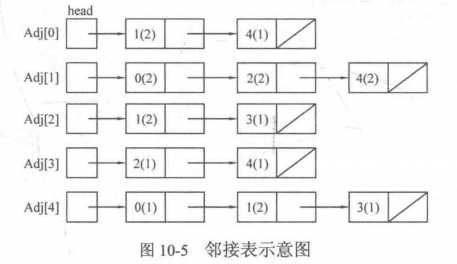
上图中,0号顶点有两条出边:一条的终点为1号顶点(边权为2);另一条边的终点为4号顶点(边权为1)。
可以使用vector来实现邻接表。可以开一个vector数组Adj[N],其中N为顶点个数。如果想添加一条从1号顶点到达3号顶点的有向边,只需要在Adj[1]中添加终点编号3即可。
Adj[1].push_back(3);
如果需要同时存放边的终点编号和边权,那么可以建立结构体Node,用来存放每条边的终点编号和边权,代码如下所示:
struct Node{ int v; //边的终点编号 int w; //边权 };
这样vector邻接表中的元素类型就是Node型的,如下所示:
vector<Node> Adj[N];
此时如果想要添加从1号到达3号顶点的有向边,边权为4,就可以定义一个Node型的临时变量temp,令temp.v = 3,temp.w = 4,然后把temp加入到Adj[1]中即可。
Node[temp];
temp.v = 3;
temp.w = 4;
Adj[1].push_back(temp);
顶点数目较大的情况下,一般都需要使用邻接报而非邻接矩阵来存储图。
10.3 图的遍历
10.3.1 采用深度优先搜索(DFS)法遍历图
1.用DFS遍历图

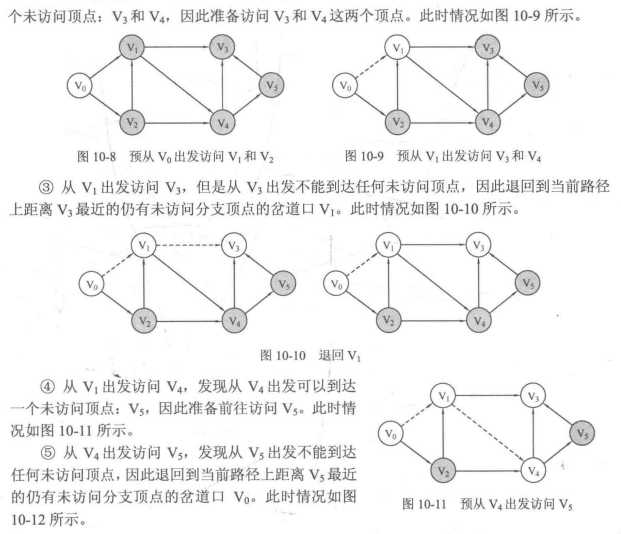
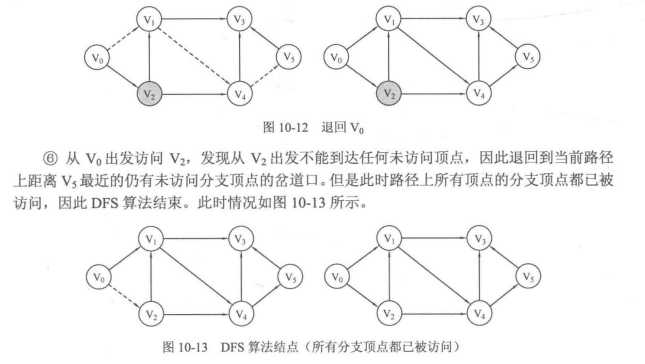
2.DFS的具体实现:
两个概念:
*连通分量:在无向图中,如果两个顶点之间可以相互到达,那么就称这两个顶点连通。如果图G(V,E)的任意两个顶点都连通,则称图G为连通图,否则,称图G为非连通图,且称其中的极大连通子图为连通分量。
*强连通分量:在有向图中,如果两个顶点可以各自通过一条有向路径到达另一个顶点,就称这两个顶点强连通。如果图G(V,E)的任意两个顶点都强连通,则称图G为强连通图;否则,称图G为非强连通图,且称其中的极大强连通子图为强连通分量。
①邻接矩阵版
const int MAXV = 1000; //最大顶点数 const int INF = 1000000000; //设INF为一个很大的数 int n,G[MAXV][MAXV]; //n为顶点数,MAXV为最大顶点数 bool vis[MAXV] = {false}; //如果顶点i已被访问,则vis[i] == true。初值为false void DFS(int u,int depth){ //u为当前访问的顶点标号,depth为深度 vis[u] = true; //如果需要对u进行一些操作,可以在这里进行 //下面对所有从u出发能到达的分支顶点进行枚举 for(int v = 0;v<n;v++){ //对每个顶点v if(vis[v] == false && G[u][v] != INF){ //如果v未被访问,且u可到达v DFS(v,depth+1); //访问v,深度加1 } } } void DFSTraver(){ //遍历图G for(int u = 0; u < n; u++){ //对每个顶点u if(vis[u] == false){ //如果u未被访问 DFS(u,1); //访问u和u所在的连通块,1表示初始为第一层 } } }
②邻接表版
const int MAXV = 1000; //最大顶点数 const int INF = 1000000000; //设INF为一个很大的数 vector<int> Adj[MAXV]; //图G的邻接表 int n; //n为顶点数,MAXV为最大顶点数 bool vis[MAXV] = {false}; void DFS(int u,int depth){ //u为当前访问的顶点标号,depth为深度 vis[u] = true; //设置u已被访问 /*如果需要对u进行一些操作,可以在此处进行*/ for(int i = 0;i < Adj[u].size();i++){ //对从u出发可以到达的所有顶点v int v = Adj[u][i]; if(vis[v] == false){ //如果v未被访问 DFS(v,depth+1); //访问v,深度加1 } } } void DFSTrave(){ //遍历图G for(int u = 0 ; u < n; u++){ //对每个顶点u if(vis[u] == false){ //如果u未被访问 DFS(u,1); //访问u和u所在的连通块,1表示初始为第一层 } } }
原文:https://www.cnblogs.com/coderying/p/12287161.html