给定一个N*M方格的迷宫,迷宫里有T处障碍,障碍处不可通过。给定起点坐标和终点坐标,问: 每个方格最多经过1次,有多少种从起点坐标到终点坐标的方案。在迷宫中移动有上下左右四种方式,每次只能移动一个方格。数据保证起点上没有障碍。
这道题着实让我感受到了玄学的强大
题意分析:
考点:dfs
每次搜索进行如下的判断:
1.这个点是否越界?
2.这个点是否走过?是否为障碍?
3.到没到终点?(如果到了,计数器加一)
注意:
以上三点不可调换顺序,不然你可以尝到30分,90分的快乐(亲自尝试)
可是为什莫会这样呢?
以下是我个人的猜测:
首先,第二点的成立必须建立在第一点成立的基础上,不然第二点的判断是无效的
其次,根据数组大小,一三点如果调换,可能会出现这样的情况:
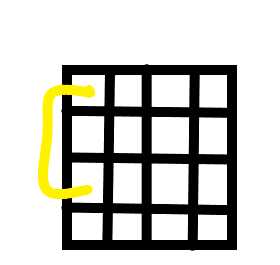
因为数据最小点为(1,1),数组从(0,0)开始,所以可能出现图中从外面绕圈的情况
总上面两点所述,第一点必须排在最前面。
至于二,三点,我想到的唯一能说明二一定要排在三前面的就是如果出现终点有障碍的情况
亲测,调换二,三点90分
综上,就能安心的把这三条用代码实现啦
然后,分别从上下左右依次递归,就能解决问题啦!
上代码:
#include<bits/stdc++.h> using namespace std; int tmp=0; int n,m,t;//n为行,m为列,t为障碍总数 int sx,sy,fx,fy;//起点坐标和终点坐标 int x,y;//障碍点坐标 int a[6][6];//建立一个地图 int p[6][6];//判断走没走过 void f(int c,int d)//dfs函数 { if(c<=0||d<=0||c>m||d>n)//防止越界 { return ; } if(a[c][d]==0||p[c][d]==0)//判断是否为障碍,走没走过,是否越界 { return; } if(c==fx&&d==fy)//找到一种方案,记录下来 { tmp++; return ; } p[c][d]=0; f(c+1,d);//向右走 f(c-1,d);//向左走 f(c,d+1);//向下走 f(c,d-1);//向上走 p[c][d]=1;//回溯,不起眼但很重要 } int main(void)//好习惯 { cin>>n>>m>>t; cin>>sx>>sy>>fx>>fy; for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { a[i][j]=1;//初始化地图 p[i][j]=1;//初始化障碍 } } for(int i=0;i<t;i++) { cin>>x>>y; a[x][y]=0;//标记障碍点 } f(sx,sy);//dfs cout<<tmp; return 0; }
(原代码有误,已改正)
总结:
在调试程序时,关注一下代码的顺序是否会造成结果的不同,特别是在有部分分的时候
the end~
原文:https://www.cnblogs.com/zhangzhiyuan123/p/12288013.html