题意:有N件物品和一个容量为M的背包。第i件物品的体积是c[i],价值是w[i]。求解将哪些物品装入背包可使价值总和最大。(不一定要将背包装满),但不能超过背包的容量。
下面给出一个具体例子便于理解:
| 物品编号 | 物体体积 | 物品价值 |
|---|---|---|
| 1 | 2 | 3 |
| 2 | 3 | 4 |
| 3 | 4 | 5 |
| 4 | 5 | 6 |
然后我将给出一个表格,橙色底纹的数据含义:在当前背包容量下,考虑前n个物品的最佳组合(不超过背包容量,不一定要装满),使得背包总价值最大,在格子中填入这个最大的总价值.
如:最右下方的格子代表在容量为8的背包中,从前4个物品选择x种物品后得到使背包内价值最大的方案,这个价值为10(将2、4放入)
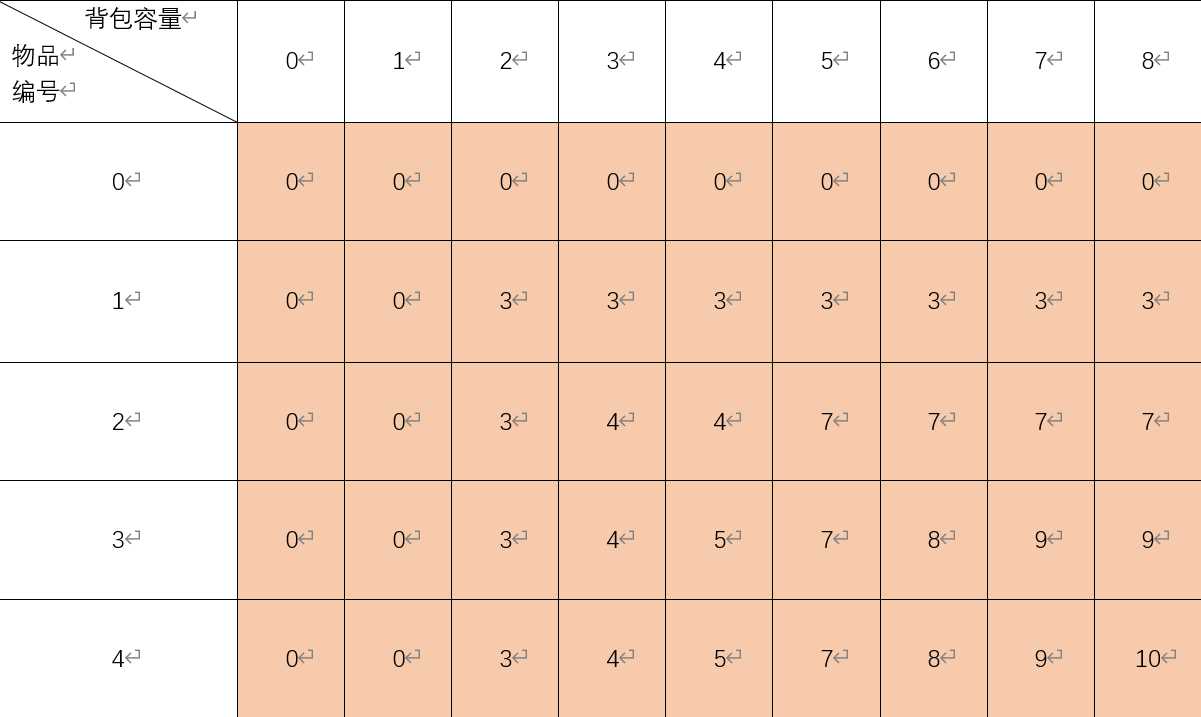
上面其实用的是二维数组的解法,在这里分析一下吧:
在这里细分有三种情况,粗劣的分有两种情况;
一.无法装下当前物品;那么说明这一次背包内物品的体积和上一次一样,也就是前n个物品的最佳组合产生的价值和前n-1个物品的最佳组合产生的价值相同.
二.可以装下当前物品;
1.选择不装当前物品:和无法装下当前物品的结果一样,前n个物品的最佳组合产生的价值和前n-1个物品的最佳组合产生的价值相同.
2.选择装当前物品:除去当前物品在该背包占用的空间所得到的空间在前n-1个物品中最佳组合产生的价值加上当前物品所产生的价值构成总价值.
接着比较1、2者2大小。
#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<stdlib.h>
#include<string.h>
#include<math.h>
using namespace std;
typedef long long LL;
const int maxn=1e5+7;
const int maxm=2e5+7;
const int maxi=1000;
const long long INF=0x3f3f3f3f;
const long long mod=1e9+7;
int n,m;
int w[maxi],d[maxi];//w[i]:第i件物品的体积,d[i]:第i件物品的价值.
int f[maxi][maxi];//f[i][j]代表在体积j下,前i个物品的最佳组合所产生的价值(最大价值)
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d%d",&w[i],&d[i]);
for(int i=1;i<=n;i++)
{
int v=1;
while(v<w[i])//当前背包的体积无法放下当前物品
{
f[i][v]=f[i-1][v];//直接将前i-1个物品最佳组合的价值赋值给前i个物品的最佳组合价值
v++;
}
for(v=w[i];v<=m;v++)//当前背包的体积可以放下当前物品
f[i][v]=max(f[i-1][v],f[i-1][v-w[i]]+d[i]);//选择将第i个物品不放入背包或者放入背包
}
printf("%d",f[n][m]);
return 0;
}
However,这道题仍然是可以进行优化的,用一个一维的滚动数组就可以达到目的。
我们不难发现,计算前n个物品的最佳组合产生的价值时,我们仅仅使用了前n-1个物品的最佳组合产生的价值,并没有用到前n-2、前n-3…的最大价值,所以我们可以直接用一维数组不断的将数组元素进行滚动替换掉即可。
#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<stdlib.h>
#include<string.h>
#include<math.h>
using namespace std;
typedef long long LL;
const int maxn=1e5+7;
const int maxm=2e5+7;
const long long INF=0x3f3f3f3f;
const long long mod=1e9+7;
int n,m;
int w[maxn],d[maxn];//w[i]:第i件物品的体积,d[i]:第i件物品的价值.
int f[maxn];
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d%d",&w[i],&d[i]);
memset(f,0,sizeof(f));//将前n个物品的最佳组合产生的价值全部初始化为0
for(int i=1;i<=m;i++)
for(int v=m;v>=w[i];v--)
f[v]=max(f[v],f[v-w[i]]+d[i]);
printf("%d",f[m]);
return 0;
}
原文:https://www.cnblogs.com/K2MnO4/p/12288568.html