给定\(n\)个数。有一种操作,选择一个数使之加一。现要求这\(n\)个数的和和积均不为0,问最少的操作次数。
有\(0\)加\(1\),最后和为\(0\)的话,因为每个数都不是\(0\),所以必有正也有负,此时再随便找一个正数加\(1\)即可。
神奇的代码
#include <bits/stdc++.h>
#define MIN(a,b) ((((a)<(b)?(a):(b))))
#define MAX(a,b) ((((a)>(b)?(a):(b))))
#define ABS(a) ((((a)>0?(a):-(a))))
using namespace std;
typedef long long LL;
typedef vector<int> VI;
typedef pair<int,int> PII;
typedef vector<PII> VPII;
typedef vector<LL> VL;
typedef pair<LL,LL> PLL;
typedef vector<PLL> VPLL;
template <typename T>
void read(T &x) {
int s = 0, c = getchar();
x = 0;
while (isspace(c)) c = getchar();
if (c == 45) s = 1, c = getchar();
while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar();
if (s) x = -x;
}
template <typename T>
void write(T x, char c = ' ') {
int b[40], l = 0;
if (x < 0) putchar(45), x = -x;
while (x > 0) b[l++] = x % 10, x /= 10;
if (!l) putchar(48);
while (l) putchar(b[--l] | 48);
putchar(c);
}
int main(void) {
int kase; read(kase);
for (int i = 1; i <= kase; i++) {
int n;
read(n);
int a[n+1]={0};
int sum=0;
int ans=0;
for(int i=1;i<=n;++i){
read(a[i]);
if (a[i]==0) ++a[i],++ans;
sum+=a[i];
}
if (sum==0) ++ans;
write(ans,'\n');
}
return 0;
}\(2*n\)个数要求分成两组,使两个组的中位数相差最小,问最小差。
很容易看出答案就是这\(2*n\)个数排好序后第\(n\)个数和第\(n+1\)个数的差值。
神奇的代码
#include <bits/stdc++.h>
#define MIN(a,b) ((((a)<(b)?(a):(b))))
#define MAX(a,b) ((((a)>(b)?(a):(b))))
#define ABS(a) ((((a)>0?(a):-(a))))
using namespace std;
typedef long long LL;
typedef vector<int> VI;
typedef pair<int,int> PII;
typedef vector<PII> VPII;
typedef vector<LL> VL;
typedef pair<LL,LL> PLL;
typedef vector<PLL> VPLL;
template <typename T>
void read(T &x) {
int s = 0, c = getchar();
x = 0;
while (isspace(c)) c = getchar();
if (c == 45) s = 1, c = getchar();
while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar();
if (s) x = -x;
}
template <typename T>
void write(T x, char c = ' ') {
int b[40], l = 0;
if (x < 0) putchar(45), x = -x;
while (x > 0) b[l++] = x % 10, x /= 10;
if (!l) putchar(48);
while (l) putchar(b[--l] | 48);
putchar(c);
}
int main(void) {
int kase; read(kase);
for (int i = 1; i <= kase; i++) {
int n;
read(n);
n<<=1;
int a[n];
for(int i=0;i<n;++i) read(a[i]);
sort(a,a+n);
int ans=a[n/2]-a[n/2-1];
write(ans,'\n');
}
return 0;
}有一函数\(f:f(x, y) = (x | y) - y\)(\(|\)是或运算并不是整除),现有\(n\)个数\(a_1,a_2,...,a_n\),要求安排一种顺序,使得\(f(f(\dots f(f(a_i, a_j), a_k), \dots a_{z}), a_n)\)结果最大。
注意到\(f\)函数可以等效为一种位运算,\(f(x,y)\),对于\(y\)的每一个是\(1\)的位,如果\(x\)对应位为\(1\)则变成\(0\),否则则不改变。所以一旦我们确定了第一个数\(a_i\),剩下的数的顺序是无关紧要的。我们统计每个数在二进制下\(1\)所在的位数,最后从高到低看哪一位的\(1\)只有一个数有,就把那个数放在第一位,其他的数随便输出就好了。因为如果出现次数是\(2\)及以上的话会被消掉。
神奇的代码
#include <bits/stdc++.h>
#define MIN(a,b) ((((a)<(b)?(a):(b))))
#define MAX(a,b) ((((a)>(b)?(a):(b))))
#define ABS(a) ((((a)>0?(a):-(a))))
using namespace std;
typedef long long LL;
typedef vector<int> VI;
typedef pair<int,int> PII;
typedef vector<PII> VPII;
typedef vector<LL> VL;
typedef pair<LL,LL> PLL;
typedef vector<PLL> VPLL;
template <typename T>
void read(T &x) {
int s = 0, c = getchar();
x = 0;
while (isspace(c)) c = getchar();
if (c == 45) s = 1, c = getchar();
while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar();
if (s) x = -x;
}
template <typename T>
void write(T x, char c = ' ') {
int b[40], l = 0;
if (x < 0) putchar(45), x = -x;
while (x > 0) b[l++] = x % 10, x /= 10;
if (!l) putchar(48);
while (l) putchar(b[--l] | 48);
putchar(c);
}
int main(void) {
int n;
read(n);
int a[n];
int cnt[35];
memset(cnt,0,sizeof(cnt));
for(int i=0;i<n;++i) {
read(a[i]);
int qwq=a[i];
int id=0;
while(qwq){
cnt[id++]+=(qwq&1);
qwq>>=1;
}
}
int id=35;
while(id>=0&&cnt[id]!=1) --id;
if (id==-1) for(int i=0;i<n;++i) printf("%d%c",a[i],i==n-1?'\n':' ');
else{
for(int i=0;i<n;++i) if ((a[i]>>id)&1){id=i;break;}
printf("%d ",a[id]);
for(int i=0;i<n;++i) if (i==id) continue; else printf("%d ",a[i]);
}
return 0;
}以给端点坐标的形式给定一个多凸边形\(P\),定义一种线性变换\(P(x,y)\)表示将多边形\(P\)分别沿\(x\)轴方向平移\(x\)个单位,沿\(y\)轴方向平移\(y\)个单位后的多边形。定义\(T\)是一连串符合条件的\(P(x,y)\)多边形的并集,条件是原点\((0,0)\)在\(P(x,y)\)的边上或里面,问\(T\)与\(P\)是否相似。
读题读了好多遍才明白……原本没有什么头绪的然后我打开几何画板把样例三的图形画出来后。
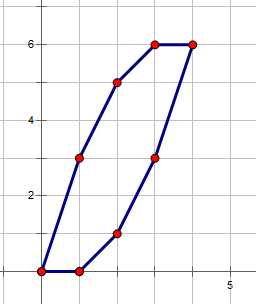
我有一个大胆的想法。
如果是奇多边形肯定不相似,偶多边形的话,就看它对边是否平行且相等。(点\(i\)与点\(i+1\)所形成的边与点\(i+\frac{n}{2}\)与点\(i+1+\frac{n}{2}\)所形成的边)
(猜题大法好)
神奇的代码
#include <bits/stdc++.h>
#define MIN(a,b) ((((a)<(b)?(a):(b))))
#define MAX(a,b) ((((a)>(b)?(a):(b))))
#define ABS(a) ((((a)>0?(a):-(a))))
using namespace std;
typedef long long LL;
typedef vector<int> VI;
typedef pair<int,int> PII;
typedef vector<PII> VPII;
typedef vector<LL> VL;
typedef pair<LL,LL> PLL;
typedef vector<PLL> VPLL;
template <typename T>
void read(T &x) {
int s = 0, c = getchar();
x = 0;
while (isspace(c)) c = getchar();
if (c == 45) s = 1, c = getchar();
while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar();
if (s) x = -x;
}
template <typename T>
void write(T x, char c = ' ') {
int b[40], l = 0;
if (x < 0) putchar(45), x = -x;
while (x > 0) b[l++] = x % 10, x /= 10;
if (!l) putchar(48);
while (l) putchar(b[--l] | 48);
putchar(c);
}
int main(void) {
int n;
read(n);
pair<int,int> point[n];
for(int x,y,i=0;i<n;++i){
read(x);
read(y);
point[i]=make_pair(x,y);
}
if (n&1) puts("NO");
else{
bool qwq=true;
for(int j=0,i=n/2;i<n;++i,++j){
if (!qwq) break;
if (point[j].first-point[j+1].first!=point[(i+1)%n].first-point[i].first) qwq=false;
if (point[j].second-point[j+1].second!=point[(i+1)%n].second-point[i].second) qwq=false;
}
if (qwq) puts("YES");
else puts("NO");
}
return 0;
}给定一个有\(n\)个数的序列,有一种操作,选择两个数\(l,r(l<r)\),然后将区间\([l,r]\)的数替换成这个区间的平均数。可以进行任意多次操作,问最后能得到的字典序最小的序列是怎样的。
我们注意到一个重要性质:最终序列的数一定是递增的。因为如果有前一个数大于后一个数,那么我们把那个范围取个平均值,得到的是一个字典序更小的序列。所以我们就从左到右依次把每个数添加进去,如果这个数小于前一个我们已经平均的平均数,那么我们就把这个数也加入到前一个平均的范围内,重复即可。
神奇的代码
#include <bits/stdc++.h>
#define MIN(a,b) ((((a)<(b)?(a):(b))))
#define MAX(a,b) ((((a)>(b)?(a):(b))))
#define ABS(a) ((((a)>0?(a):-(a))))
using namespace std;
typedef long long LL;
typedef vector<int> VI;
typedef pair<int,int> PII;
typedef vector<PII> VPII;
typedef vector<LL> VL;
typedef pair<LL,LL> PLL;
typedef vector<PLL> VPLL;
template <typename T>
void read(T &x) {
int s = 0, c = getchar();
x = 0;
while (isspace(c)) c = getchar();
if (c == 45) s = 1, c = getchar();
while (isdigit(c)) x = (x << 3) + (x << 1) + (c ^ 48), c = getchar();
if (s) x = -x;
}
template <typename T>
void write(T x, char c = ' ') {
int b[40], l = 0;
if (x < 0) putchar(45), x = -x;
while (x > 0) b[l++] = x % 10, x /= 10;
if (!l) putchar(48);
while (l) putchar(b[--l] | 48);
putchar(c);
}
int main(void) {
int n;
read(n);
LL a[n+1]={0};
for(int i=1;i<=n;++i) read(a[i]);
pair<pair<LL,LL>,int> qwq[n+1];
int cnt=0;
qwq[0]=(make_pair(make_pair(a[1],1),1));
for(int i=2;i<=n;++i){
if (qwq[cnt].first.first>=(LL)qwq[cnt].first.second*a[i]){
qwq[cnt]=make_pair(make_pair(qwq[cnt].first.first+a[i],qwq[cnt].first.second+1),i);
while(cnt>0&&qwq[cnt].first.first*qwq[cnt-1].first.second<=qwq[cnt-1].first.first*qwq[cnt].first.second) qwq[cnt-1]=make_pair(make_pair(qwq[cnt].first.first+qwq[cnt-1].first.first,qwq[cnt].first.second+qwq[cnt-1].first.second),qwq[cnt].second),--cnt;
}
else qwq[++cnt]=make_pair(make_pair(a[i],1),i);
}
cnt=0;
for(int i=1;i<=n;++i){
printf("%.9f\n",(double)qwq[cnt].first.first/(double)qwq[cnt].first.second);
if (qwq[cnt].second==i) ++cnt;
}
return 0;
}Codeforces Round #618 (Div. 2)
原文:https://www.cnblogs.com/Lanly/p/12292092.html