题目:https://leetcode-cn.com/problems/unique-binary-search-trees-ii/
给定一个整数 n,生成所有由 1 ... n 为节点所组成的二叉搜索树。
思路:还是要从递归的角度去思考,策略是,从1-n中选择i作为根节点,那么1-i-1作为它的左子树,i+1-n作为它的右子树,1-i-1生成的BST的个数乘以i+1-n生成的BST的个数就是以i为根节点得到的BST的个数。
这里的递归调用如图:
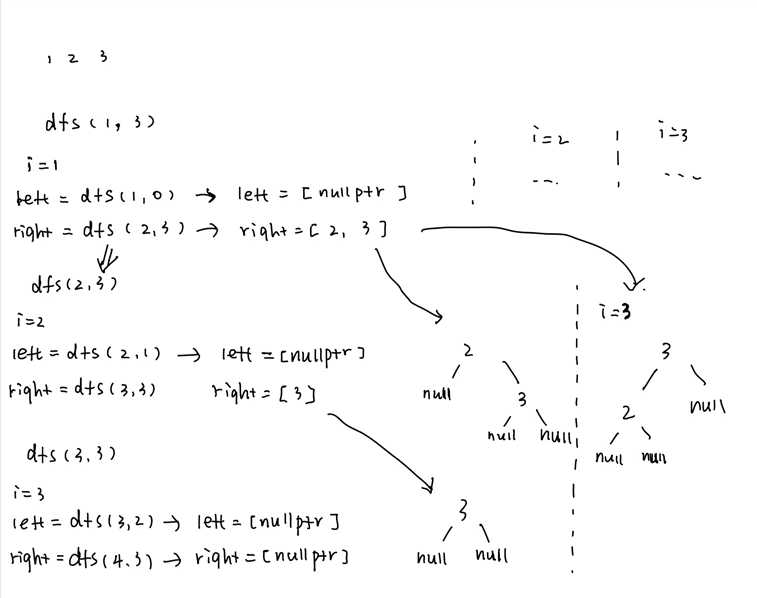
代码:
class Solution {
public:
vector<TreeNode*> dfs(int l, int r){
vector<TreeNode*> res;
if(l > r){
res.push_back(nullptr);
return res;
}
for(int i = l; i <= r; ++i){
vector<TreeNode*> left = dfs(l, i-1);
vector<TreeNode*> right = dfs(i+1, r);
for(auto &l:left){
for(auto &r:right){
TreeNode* root = new TreeNode(i);
root->left = l;
root->right = r;
res.push_back(root);
}
}
}
return res;
}
vector<TreeNode*> generateTrees(int n) {
if(n == 0) return vector<TreeNode*>();
else return dfs(1, n);
}
};原文:https://www.cnblogs.com/patrolli/p/12293368.html