11.1 动态规划的递归写法和逆推写法
动态规划没有固定的写法、极其灵活,常常需要具体问题具体分析。
11.1.1 什么是动态规划
动态规划将一个复杂的问题分解成若干个子问题,通过综合子问题的最优解来得到原问题的最优解。
11.1.2 动态规划的递归写法
如下是斐波那契数列的常规写法
int F(int n){ if(n == 0 || n == 1) return 1; else return F(n-1) + F(n-2); }
但这种写法会涉及很多重复的计算,当n == 5时,可以得到F(5) = F(4) + F(3),接下来在计算F(4) 时又会有F(4) = F(3) + F(2).这时,F(3)被计算了两次。如果n很大,重复计算的次数将难以想象。
可以开一个一维数组dp[n]用以保存已经计算过的结果,其中dp[n]记录F(n)的结果,并用dp[n] = -1表示F(n)当前还没有被计算过。
int dp[MAXN]; int F(int n){ if(n == 0 || n == 1) return 1; if(dp[n] != -1) return dp[n]; else{ dp[n] = F[n-1] + F[n-2]; return dp[n]; } }
如果一个问题可以被分解为若干个子问题,且这些子问题会重复出现,那么就称这个问题拥有重叠子问题。动态规划通过记录重叠子问题的解,来使下次碰到相同的子问题时直接使用之前记录的结果,以此避免大量重复计算。
11.1.3 动态规划的递推写法
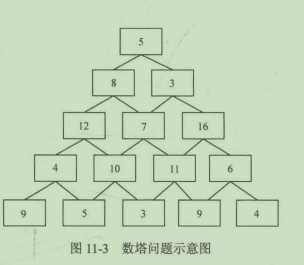
求上图中路径上所有数字相加后得到的和最大是多少?
#include<cstdio> #include<algorithm> using namespace std; const int maxn = 1000; int f[maxn][maxn],dp[maxn][maxn]; int main(){ int n; scanf("%d",&n); for(int i=1;i <= n;i++){ for(int j = 1; j <= i;j++){ scanf("%d",&f[i][j]); } } //边界 for(int j = 1; j <= n;j++){ dp[n][j] = f[n][j]; } //从第n-1层不断往上计算出dp[i][j] for(int i = n - 1; i >= 1 ;i--){ for(int j =1; j <= i;j++){ //状态转移方程 dp[i][j] = max(dp[i+1][j],dp[i+1][j+1]) + f[i][j]; } } printf("%d\n",dp[1][1]); return 0; }
通过例子再引申出一个概念:如果一个问题的最优解可以由其子问题的最优解有效地构造出来,那么称这个问题拥有最优子结构。
一个问题必须拥有重叠子问题和最优子结构,才能使用动态规划去解决。
11.2 最大连续子序列和
给定一个数字序列A1,A2,...,An,求i,j (1 <= i <= j <= n),使得Ai + ..... + Aj最大,输出这个最大和。
样例:
-2 11 -4 13 -5 -2
显然11+(-4) + 13 = 20为和最大的选取情况,因此最大和为20.
用动态规划求解:
步骤1:令状态dp[i]表示以A[i]作为末尾的连续序列的最大和。以样例为例:序列-2 11 -4 13 -5 -2,下标分别记为0,1,2,3,4,5,那么
dp[0] = -2;
dp[1] = 11;
dp[2] = 7 (11 + (-4) = 7);
dp[3] = 20 (11 + (-4) + 13 = 20)
dp[4] = 15
dp[5] = 13
步骤2: 因为dp[i]要求是必须以A[i]结尾的连续序列,那么只有两种情况:
①这个最大和的连续序列只有一个元素,即以A[i]开始,以A[i]结尾。
②这个最大和的连续序列有多个元素,即从前面某处A[p] 开始,一直到A[i]结尾。
可以得到状态转移方程:dp[i] = max{A[i] , dp[i-1] + A[i] }
因此,实现代码如下:
#include<cstdio> #include<algorithm> using namespace std; const int maxn = 10010; int A[maxn],dp[maxn]; int main(){ int n; scanf("%d",&n); for(int i = 0; i < n;i++){ scanf("%d",&A[i]); } //边界 dp[0] = A[0]; for(int i = 1; i < n;i++){ //状态转移方程 dp[i] = max(A[i],dp[i-1] + A[i]); } //dp[i]存放以A[i]结尾的连续序列的最大和,需要遍历i得到最大的才是结果 int k = 0; for(int i = 1;i < n;i++){ if(dp[i] > dp[k]){ k = i; } } printf("%d\n",dp[k]); return 0; }
状态的无后效性:当前状态记录了历史信息,一旦当前状态确定,就不会再改变,且未来的决策只能在已有的一个或者若干个状态的基础上进行,历史信息只能通过已有的状态去影响未来的决策。
动态规划的核心:如何设计状态和状态转移方程
11.3 最长不下降子序列(LIS)
算法笔记 第11章 提高篇(5) --动态规划专题 学习笔记
原文:https://www.cnblogs.com/coderying/p/12293481.html