关于 二阶非齐次常系数线性微分方程 特解 的解法

考研期间遇到的一个很强大的解题技巧，但是步骤依然要用待定系数法写，不然没有过程分（口口相传，待考证），不过熟练掌握此方法可以极大的节约答题时间，遂本人讲看到的几份对自己收获大的资料进行总结整理，本着分享学习精神，写出以下文章。如有谬误，望大家不吝赐教。

若并不关心原理证明之类的，则可以直接看性质，或看例题（虽然我这么懒大概率不会往上敲例题）。

希望能给各位带来帮助，难理解之处我会添加注释 //

一、定义

二阶非齐次常系数线性微分方程的一般形式如下：
\[ \frac{d^2y}{dx^2}+p\frac{dy}{dx}+qy=f(x)，(p、q为常数) \]
引入微分算子：
\[ \frac{d}{dx}=D，\frac{d^2}{dx^2}=D^2，\cdots，\frac{d^n}{dx^n}=D^n \]
于是有：
\[ \frac{dy}{dx}=Dy，\frac{d^2y}{dx^2}=D^2y，\cdots，\frac{d^ny}{dx^n}=D^ny\\frac{1}{D^n}=\underbrace{\int\cdots\int}_{共n次} f(x)(dx)^n\\frac{1}{D+K}f(x)=\frac{1}{K}(1-\frac{D}{K}+\cdots+(-1)^n\frac{D^n}{K^n}+\cdots)f(x) \]
则(1)式可以简化为：
\[ \begin{align} f(x)&=qy+pDy+D^2y\&=(D^2+pD+q)y\::&=F(D)y，称F(D)为“算子多项式” \end{align} \]
则式（1）的特解\(y^*\)为：
\[ y^*=\frac{1}{F(D)}f(x) \]

二、引理若干

这些我才懒得证明，别想了哼 (ˉ▽￣～)

2.1.1 算子多项式性质

设\(f(x)、g(x)\)为可微函数：则有

• \(F(D)[\alpha f(x)+\beta g(x)]=\alpha F(D)f(x)+\beta F(D)g(x)\)
• 设\(F(D)=F_1(D)F_2(D)\)，则有\(F(D)f(x)=F_1(D)[F_2(D)f(x)]=F_2(D)[F_1(D)f(x)]\)
• 设\(F(D)=F_1(D)+F_2(D)\)，则\(F(D)f(x)=F_1(D)f(x)+F_2(D)f(x)\)

2.1.2 算子多项式の公式

设k,a为任意常数，v(x)为二阶可导多项式，则

• \(F(D)e^{kx}=e^{kx}F(k)\)
• \(F(D^2)\sin{ax}=\sin{ax}F(-a^2)、F(D^2)\cos{ax}=\cos{ax}F(-a^2)\)
• \(F(D)e^{kx}v(x)=e^{kx}F(D+k)v(x)\)
• \(F(D)xv(x)=xF(D)v(x)+F'(D)v(x)\)

三、一些性质

3.1 逆算子移位原理

\[ \frac{1}{F(D)}e^{kx}v(x)=e^{kx}\frac{1}{F(D+k)}v(x) \]

• 若\(F(k)\neq0\)，则：

\[ \frac{1}{F(D)}e^{kx}=e^{kx}\frac{1}{F(k)}，此时F(k)已然是数值 \]

• 若\(F(k)=0\)，则说明 k 为\(F(k)=0\) 的 m 重根，则有：

\[ \frac{1}{F(D)}e^{kx}=x^m\frac{e^{kx}}{F^{(m)}(k)} \]

3.2 关于三角函数

欧拉公式：
\[ e^{r\beta x}=\cos{\beta x}+i\sin{\beta x}\\cos{\beta x}=Re[e^{i\beta x}]，称为实部\\sin{\beta x}=Im[e^{i\beta x}]，称为虚部 \]

• 当\(F(-a^2)\neq0\)时：

\[ \frac{1}{F(D^2)}\sin{ax}=\frac{\sin{ax}}{F(-a^2)}\\frac{1}{F(D^2)}\cos{ax}=\frac{\cos{ax}}{F(-a^2)}\\]

• 当\(F(-a^2)=0\)时：

\[ \frac{1}{F(D^2)}\sin{ax}=x\frac{1}{F'(D^2)}\sin{ax}\\frac{1}{F(D^2)}\cos{ax}=x\frac{1}{F'(D^2)}\cos{ax}\\]

• \[ \frac{1}{F(D^2)}\sin{ax}=Im[\frac{e^{iax}}{F(ia)}]\\frac{1}{F(D^2)}\cos{ax}=Re[\frac{e^{iax}}{F(ia)}]\\]

3.3 含多项式的情况

设 k 为任意实数，v（x）为二阶可导函数，则：

\[ \frac{1}{F(D)}P_m(x)=Q_m(D)P_m(x) \]

\[ \frac{1}{F(D)}xv(x)=[x-\frac{1}{F(D)}F'(D)]\frac{1}{F(D)}v(x) \]

四、 公式（8）~（16）证明

引理（1）：若\(p(x)\)为多项式，\(v(x)\)为任意函数，那么有：
\[ p(D)e^{\lambda x}v(x)=e^{\lambda x}p(D+\lambda)v(x) \]

引理（2）：设\(f_p(x)\)为 p 次多项式，即\(f_p(x)=a_0x^p+a_1x^{p-1}+\cdots+a_p\)，那么：
\[ \frac{1}{\prod_{i=1}^m(D+K)}f_p(x) \]
仍为 p 次多项式。

\[ \begin{align} &\because\frac{1}{D+K_1}f(x)=\frac{1}{K_1}(\frac{1}{1+\frac{D}{K_1}})f_p(x)=\frac{1}{K_1}(1-\frac{D}{K_1}+\cdots+(-1)^n\frac{D^n}{K_1^n}+\cdots)f_p(x)\&\because D^{n+1}f_p(x)=0,\&\therefore \frac{1}{D+K_1}f(x)=\frac{1}{K_1}(1-\frac{D}{K_1}+\cdots+(-1)^n\frac{D^n}{K_1^n})f_p(x)\&\therefore\frac{1}{\prod_{i=1}^m(D+K_i)}f_p(x)=[\frac{1}{D+k_m}[\cdots[\frac{1}{D+K_1}f_p(x)]]]，仍为p次多项式 \end{align} \]

五、 一些例子

1. \(\frac{d^2y}{dx^2}+y=x\cos{2x}，F(D)=1+D^2\)

\[ \begin{align} 特解：y^*&=\frac{1}{1+D^2}x\cos{2x}\&=Re[\frac{1}{1+D^2}xe^{2ix}]\&=Re[e^{2ix}\frac{1}{1+(D+2i)^2}x]，移位原理\&=Re[e^{2ix}\frac{1}{D^2+4iD-3}x]，（*）这一步我会贴图\&=Re[e^{2ix}(-\frac{1}{3}-\frac49iD)x]\&=Re[(\cos{2x}+i\sin{2x})(-\frac{1}{3}x-\frac49i)],D::=\frac{dy}{dx}\&=\frac{1}{3}x\cos{2x}+\frac{4}{9}\sin{2x} \end{align} \]

六、引用

• [1] 《常微分方程》王高雄、高等教育出版社“高阶微分方程中的拉普拉斯变换方法”
• [2 ] “"二阶常系数线性微分方程特解的微分算子法" 李绍刚、徐安农”桂林电子科技大学学报“

关于二阶非齐次常系数线性微分方程特解的解法

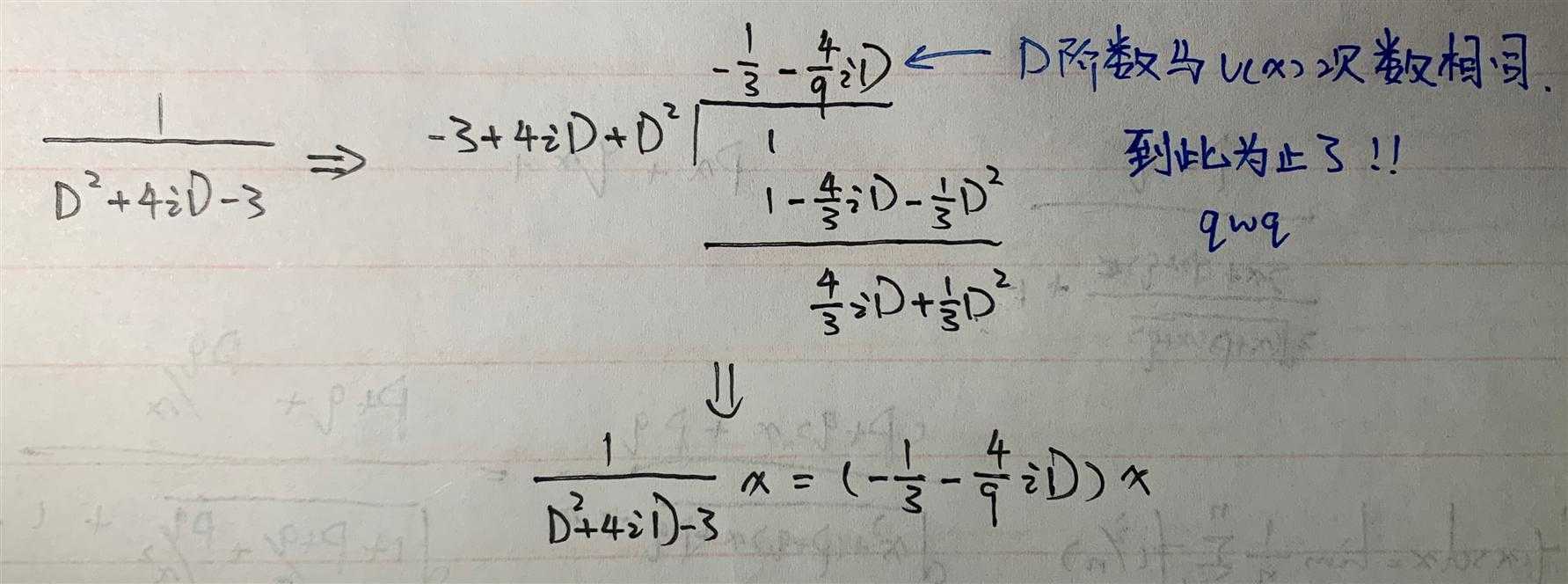
原文：https://www.cnblogs.com/rrrrraulista/p/12293670.html