树的重心 学习笔记

第一版

关于树的重心

1. 有配图
2. 有文字讲解

关于Godfather

1. 有AC代码
2. 文字说明

关于centroid

1. 本人蒟蒻这晚上只写了55pts(以后会有AC代码的)
2. 手把手教你分析时间复杂度
3. 考场写暴力得省一心得
4. 有了树的重心的性质拓展

树的重心

在树的问题中，会遇到一些题目。时问你树的重心的，不会就凉了,就像CSP-S2019

定义

度娘的定义是这样的 ： 找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后，生成的多棵树尽可能平衡。

性质

1. 树中所有点到某个点的距离和中，到重心的距离和是最小的，如果有两个重心，他们的距离和一样。
2. 把两棵树通过一条边相连，新的树的重心在原来两棵树重心的连线上。
3. 一棵树添加或者删除一个节点，树的重心最多只移动一条边的位置。
4. 一棵树最多有两个重心，且相邻。
5. 事实上，有个性质度娘没说，在centroid中提到了

Godfather

原题链接

这道题

我们可以用树形dp来解决这个问题令\(d_i\)表示你把他转为有根树之后以\(i\)为根的子树所包含节点个数

采用邻接表存边，我们能可以十分简单的解决此问题

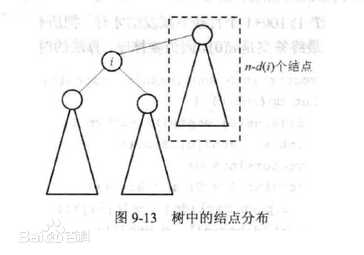
我们判断一个点是否树的重心的方法是去掉这个点所有子树的最大连通块最小

事实上，这些连通块就是，这个节点上面的部分和以这个点所有儿子为根的子树的最大值

这是AC代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
const int Maxn=50005;
int n,d[Maxn],h[Maxn],cnt,u,v,a[Maxn],num,min1; 
struct Edge{
    int fr,to,lac;
    void insert(int x,int y){
        fr=x;
        to=y;
        lac=h[x];
        h[x]=cnt++;
    }
}edge[Maxn*2];
int read(){
    int x=0;
    char ch=getchar();
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch<='9'&&ch>='0'){
        x=(x<<1)+(x<<3)+(ch-'0');
        ch=getchar();
    }
    return x;
}
void dfs(int u,int fa){
    //树形dp 
    int max1=0;d[u]=1;
    //就是他的尺寸
    for(int i=h[u];i!=-1;i=edge[i].lac){
        if(edge[i].to==fa) continue;
        dfs(edge[i].to,u);
        d[u]+=d[edge[i].to];
        //加上子树 
        max1=max(max1,d[edge[i].to]);
    }
    max1=max(max1,n-d[u]);
    //得出最大连通块 
    if(max1<min1){
        min1=max1;
        num=1;
        a[num]=u;
    }
    else if(max1==min1) a[++num]=u;
    return ;
}
int main(){
    //freopen("MRK.in","r",stdin);
    n=read();
    memset(h,-1,sizeof h);
    for(int i=1;i<n;i++){
        u=read();v=read();
        edge[cnt].insert(u,v);
        edge[cnt].insert(v,u);
    }
    //建树
    min1=n+1;
    dfs(1,-1);
    sort(a+1,a+1+num);
    for(int i=1;i<=num;i++) printf("%d ",a[i]);
    return 0;
}

Q:为什么存答案的的数组要开到很大？树的重心不最多两个吗

A: 你一开始时求出的不一定是树的重心，也就可能会很多，开太小会RE

Q:为什么答案要进行排序？

A: 树形dp ，不保证字典序最小

Q: min1 有什么用？为什么要给n+1

A: min1是记录最大连通块的最小点数，刚开始要给最小值

这里我们给出第五个性质

1. 对于一个大小为 n 的树与任意一个树中结点 c，称 c 是该树的重心当且仅当在树中删去 ccc 及与它关联的边后，分裂出的所有子树的大小均不超过 $[\frac {n} {2}] $（其中 $[\frac {n} {2}] $是下取整函数）。对于包含至少一个结点的树，它的重心只可能有 1 或 2 个。

于是我们在41至46行进行优化，避免多次记录无用信息

if(max1<=min1) a[++num]=u;

这会快一些

CSP-S 2019 D2T3 树的重心

部分测试数据下载

原题请点

这题十分的坑，以至于本蒟蒻在考场上只写出了链的特判。。。靠着我逆天的暴力。。

我们能对于40pts的小数据做一个简单的分析

1. 建图
2. 枚举每次断边
3. 对于每次断边分出的两个图分别跑树的重心
4. 这里写要注意的是n他不是本来的n,而应该先跑一边bfs ，跑出分出的树的大小，注意分开后的树
5. 统计答案

在考虑链的15pts

1. 建图
2. 跑一个链，做一个nxt[],表示后驱，做好映射
3. 然后枚举每次断的边，找到节点中间的节点，即为重心

再想想二叉树的20pts

1. 待补充

正解

1. 待补充

#include <iostream>
#include <bits/stdc++.h>
#include<queue>
using namespace std;
const int Maxn=49992;
int n,d[Maxn],t,h[Maxn],cnt,u,v,a[Maxn],num,min1,nown;
long long ans;
bool vis[Maxn];
struct Node{
    int fr,to,lac;
    bool can;
    void insert(int x,int y){
        fr=x;
        to=y;
        lac=h[x];
        h[x]=cnt++;
    }
}edge[2*Maxn];
int read(){
    int x=0;
    char ch=getchar();
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch<='9'&&ch>='0'){
        x=(x<<1)+(x<<3)+(ch-'0');
        ch=getchar();
    }
    return x;
}
void dfs(int u,int fa){
    //树形dp 
    int max1=0;d[u]=1;
    //就是他的尺寸
    for(int i=h[u];i!=-1;i=edge[i].lac){
        if(edge[i].to==fa||edge[i].can) continue;//断了，不能走 
        dfs(edge[i].to,u);
        d[u]+=d[edge[i].to];
        //加上子树 
        max1=max(max1,d[edge[i].to]);
    }
    max1=max(max1,nown-d[u]);
    //得出最大连通块 
    if(max1<=min1) a[++num]=u;
    return ;
}
void bfs(int u){
    //从源节点开始
    nown=0;memset(vis,0,sizeof vis);
    queue<int> q;
    q.push(u);vis[u]=1;
    while(!q.empty()){
        nown++;
        int fr=q.front();
        q.pop();
        for(int i=h[fr];i!=-1;i=edge[i].lac){
            if(vis[edge[i].to]||edge[i].can) continue;
            q.push(edge[i].to);
            vis[edge[i].to]=1;
        }
    } 
}
int main() {
    freopen("MRK.in","r",stdin); 
    t=read();
    while(t--){
        n=read();
        if(n==49991){
            ans=0;cnt=0;
            memset(vis,0,sizeof vis);
            memset(d,0,sizeof d);
            memset(h,-1,sizeof h);
            for(int i=1;i<n;i++){
                u=read();v=read();
                edge[cnt].insert(u,v);
                edge[cnt].insert(v,u);
                d[u]++,d[v]++;
            }
            for(int i=1;i<+n;i++)
                if(d[i]==1){
                    a[1]=i;
                    break;
                }
            vis[a[1]]=1;
            int i=1;
            while(i<n){
                int v=-1;
                for(int q=h[a[i]];q!=-1;q=edge[q].lac){
                    if(!vis[edge[q].to]){
                        v=edge[q].to;
                        vis[edge[q].to]=1;
                        break;
                    }
                }
                i++;
                a[i]=v;
            }
            for(int k=1;k<n;k++){
                if(!((1+k)&1)){
                    ans+=a[(1+k)/2];
                }
                else {
                    ans+=(a[(1+k)/2]+a[(1+k)/2+1]);
                }
                if(!((n+k+1)&1)){
                    ans+=a[(n+k+1)/2];
                }
                else {
                    ans+=(a[(n+k+1)/2]+a[(n+k+1)/2+1]);
                }
            }
            printf("%lld\n",ans);
        }
        else {
            memset(h,-1,sizeof h);cnt=0;ans=0;
            for(int i=1;i<n;i++){
                u=read();v=read();
                edge[cnt].insert(u,v);
                edge[cnt].insert(v,u);
            }
            //建树
            //从每一条边断开始枚举
            for(int i=0;i<cnt;i+=2){
                num=0; 
                edge[i].can=edge[i^1].can=1;
                //先做广搜来确定两颗子树的分别节点个数
                bfs(edge[i].fr);min1=nown/2;
                dfs(edge[i].fr,-1);
                for(int j=1;j<=num;j++) ans+=a[j];
                num=0;nown=n-nown;min1=nown/2;
                dfs(edge[i].to,-1);
                for(int j=1;j<=num;j++) ans+=a[j];
                edge[i].can=edge[i^1].can=0; 
            }
            printf("%lld\n",ans);
        }
    }
    return 0;
}

考场心得

事实上写这个md是NCP时期的无奈之举且考试确实过去不短了，自己想想还是写一些考试时的想法和学习心得吧

1. NOIP的题的特点就是贼长，要仔细读题，分析清楚
2. 实在不行就打暴力
3. 暴力不会的话，就拿部分分，甚至小数据打表
4. 其实考试前一年都没怎么学 包括oi,包括文化课，还是不要陷入感情吧，免得遗憾，免得消沉
5. 平常多练习，与同学交流看法，膜拜大神

其实，个人的心愿就是考场上遇到题，就能看出算法。。

希望这不是痴心妄想

嵬

就算有再多不顺，也要开心的过每一天。

flag :两周以内会有第二版

树的重心 学习笔记

原文：https://www.cnblogs.com/zhltao/p/12297474.html