Blocks（区间dp）

Blocks（POJ）

Description

你们中的一些人可能玩过一个叫做消木块的游戏。

n个木块排成一列，每个木块都有一个颜色。

例如下图中木块的颜色分别为：金，银，银，银，银，铜，铜，铜，金。

每次，你都可以点击一个木块，这样被点击的木块以及和它相邻并且同色的木块就会消除。

如果一次性消除了k个木块，那么就会得到k*k分。

例如下图所示，点击银色木块，四个木块被消去，得到16分。

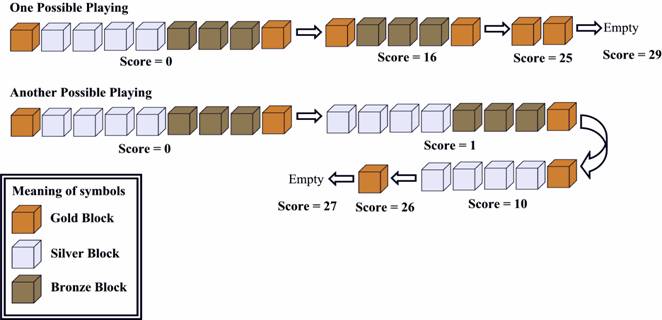
给定你一个游戏初始状态，请你求出最高得分是多少。

输入格式

第一行包含整数t，表示共有t组测试数据。

每组数据第一行包含整数n，表示共有n个木块。

第二行包含n个整数，表示n个木块的颜色。

代表木块颜色的整数范围是1~n。

输出格式

每组数据输出一个结果，每个结果占一行。

输出格式为“Case x: y”，其中x为数据组别编号，从1开始，y为结果。

数据范围1≤n≤200

Sol

首先有个显然的优化

连续一段相同颜色的木块肯定会同时被消除

于是先预处理一下得到b[i]表示第i段连续相同木块的颜色，b_l[i]表示这一段木块的个数

按照区间DP的套路设f[l][r]为消去区间l~r可以得到的最高分

但可能删去中间一段再消去，这个玩法有点棘手；

考虑枚举删去的中间一段的左右端，会有四层循环，复杂度暴了，而且删去后为新的一段木块，不符合无后效性

思考问题的分治过程：

• 删去中间一段，合并两端剩下的，使出现新的一段连续相同木块(只有这样才能得到更优的答案）
• 删去剩下的一段

这两个子问题的相似性在于都有新的l,r

另外后者出现另一个状态：删去中间段后 右边一段从左起 连续与 左边一段右端 相同的木块个数 令它为k

而前者的k即为0

于是有了dp方程（注意与上面分析的问题有点不同，它考虑了原问题有k）

f[l][r][k]=max(f[l][i][k+bl[r]]+f[i+1][r-1][0])        （b[i]==b[r] 因为这样才能使答案更优）

　　　　　　                   上文中中间一段

另外记得考虑直接把r和k消去的情况：f[l][r][k]=f[l][r-1][0]+(b[r]+k)^2

这个问题启发我们从分治过程中找灵感和牢记dp三要素，三前提

Code

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
const int N=201;
int T,n,b[N],b_l[N],f[N][N][N],tot,x,t;
int solve(int l,int r,int k)
{
    if(f[l][r][k]) return f[l][r][k];
    if(l==r) return (b_l[l]+k)*(b_l[l]+k);
    f[l][r][k]=solve(l,r-1,0)+solve(r,r,k);
    for(int i=l;i<r;i++)
        if(b[i]==b[r])
            f[l][r][k]=max(f[l][r][k],solve(l,i,k+b_l[r])+solve(i+1,r-1,0));
    return f[l][r][k];
}
int main()
{
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        tot=0;
        memset(f,0,sizeof(f));
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&x);
            if(x!=b[tot]) b[++tot]=x,b_l[tot]=1;
            else b_l[tot]++;
        }
        printf("Case %d: %d\n",++t,solve(1,tot,0));
    }
    return 0;
}

Blocks（区间dp）

原文：https://www.cnblogs.com/hsez-cyx/p/12301018.html