内容太多,捡重要的讲。
在分类问题中,通常用离散的数值表示类别,这里存在两个问题。1.输出值的范围不确定,很难判断值的意义。2.真实标签是离散值,这些离散值与不确定的范围的输出值之间的误差难以衡量。
softmax运算符解决了这两个问题。它把输出值变成了值为正且和为1的概率分布。
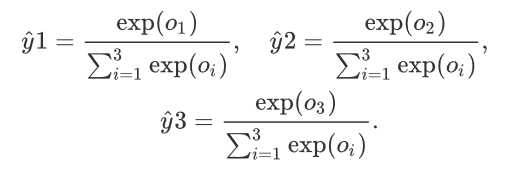
对于一个分类问题,假设有a个特征,b个样本,c个输出,单层的全连接网络,那么有a*b个w(权重),c个b(偏差)。
为了提升计算效率,常对小批量数据做矢量计算。softmax回归的矢量计算表达式如下。
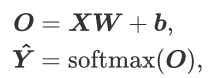
计算loss用交叉熵损失函数,如下:

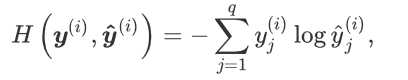
最后讲讲softmax的简洁实现:
import torch from torch import nn from torch.nn import init import numpy as np import sys sys.path.append("/home/kesci/input") import d2lzh1981 as d2l from collections import OrderedDict batch_size = 256 train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size) num_inputs = 784 num_outputs = 10 class LinearNet(nn.Module): def __init__(self, num_inputs, num_outputs): super(LinearNet, self).__init__() self.linear = nn.Linear(num_inputs, num_outputs) def forward(self, x): # x 的形状: (batch, 1, 28, 28) y = self.linear(x.view(x.shape[0], -1)) return y class FlattenLayer(nn.Module): def __init__(self): super(FlattenLayer, self).__init__() def forward(self, x): # x 的形状: (batch, *, *, ...) return x.view(x.shape[0], -1) net = nn.Sequential( # FlattenLayer(), # LinearNet(num_inputs, num_outputs) OrderedDict([ (‘flatten‘, FlattenLayer()), (‘linear‘, nn.Linear(num_inputs, num_outputs))]) init.normal_(net.linear.weight, mean=0, std=0.01) #参数初始化 init.constant_(net.linear.bias, val=0) loss = nn.CrossEntropyLoss() optimizer = torch.optim.SGD(net.parameters(), lr=0.1) num_epochs = 5 d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, optimizer)
代码摘自平台。
原文:https://www.cnblogs.com/ljwgis/p/12301434.html