图像处理一般分为空间域处理和频率域处理
空间域处理是直接对图像内的像素进行处理。主要划分为灰度变换核空间滤波两种形式,
灰度变换对图像内的单个像素进行处理,滤波处理涉及对图像质量的改变
频率域处理是先将图像变换到频率域,然后在频率域对图像进行处理,最后通过反变换将图像变为空间域。
傅里叶变换可以将图像变换为频率域, 傅立叶反变换将频率域变换为空间域
时域是以时间为坐标轴表示动态信号的关系, 频域则是把信号变为一频率为坐标轴表示出来。
时域是实际存在的,而频域则是数学构造。
numpy实现傅里叶变换
函数
dst = numpy.fft.fft2(src)
dst为一个复数数组
src 原始图像的类型应是灰度图像
该函数处理之后就能得到图像的频谱信息
零频率分量位于频谱图像的左上角
函数
dst = numpy.ffr.fftshift(src)
使用该函数处理后,图像频谱中的零频率分量会被移到频域图像的中心位置
对图像傅里叶变换后得到的是一个复数数组,为了显示图像需要将他们的值调整到 [0 , 255 ] 的灰度空间
公式为
像素新值 = 20 * np.log( np.abs( 频谱值 ) )
1 import cv2 2 import numpy as np 3 import matplotlib.pyplot as plt 4 img = cv2.imread("/home/miao/dog.jpg", 0) 5 f = np.fft.fft2(img) 6 fshift = np.fft.fftshift(f) 7 f_img = 20 * np.log(np.abs(f)) 8 magnitude_spectrum = 20 * np.log(np.abs(fshift)) 9 plt.subplot(221) 10 plt.imshow(img , cmap = ‘gray‘) 11 plt.title(‘original‘) 12 plt.axis(‘off‘) 13 plt.subplot(222) 14 plt.imshow(f_img , cmap = ‘gray‘) 15 plt.title(‘f_img‘) 16 plt.axis(‘off‘) 17 plt.subplot(223) 18 plt.imshow(magnitude_spectrum , cmap = ‘gray‘) 19 plt.title("magnitude_spectrum") 20 plt.axis(‘off‘) 21 plt.show()
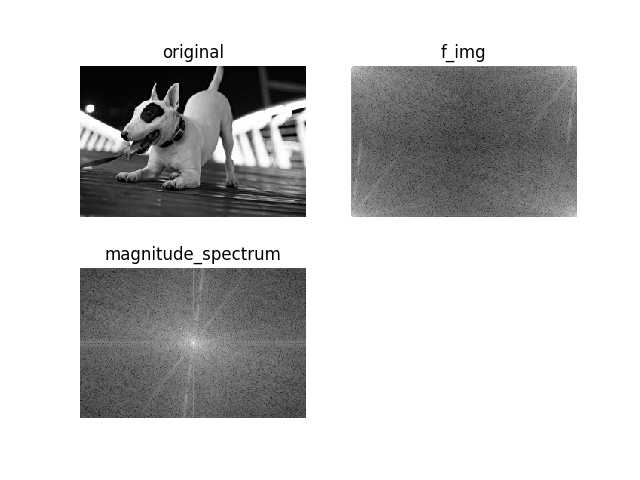
书上和查到的一些资料说傅里叶变换后的图像频谱的零频率分量位于频谱图像的左上角
通过实际操作后得到的图像 f_img 所示 零频率分量分布于四个角, 不知为何,望指教!
magnitude_spectrum可以看到中间白色区域,表示低频内容更多
实现逆傅里叶变换
numpy.fft.fftshift()函数移动了零频率分量,在逆傅里叶变换中需要使用numpy.fft.ifftshift()函数将零频率分量一道原来位置
在进行逆傅里叶变换
函数numpy.fft.ifft2() 是先逆傅里叶变换 返回值仍旧是一个复数数组
需要将信息调整至[ 0 , 255 ]灰度空间内, 使用公式
iimg = np.abs( 逆傅里叶变换结果)
1 import cv2 2 import numpy as np 3 import matplotlib.pyplot as plt 4 img = cv2.imread("/home/miao/dog.jpg", 0) 5 f = np.fft.fft2(img) 6 fshift = np.fft.fftshift(f) 7 ishift = np.fft.ifftshift(fshift) 8 iimg = np.fft.ifft2(ishift) 9 print(img) 10 iimg = np.abs(iimg) 11 print(iimg) 12 plt.subplot(121) 13 plt.imshow(img , cmap = ‘gray‘) 14 plt.title(‘original‘) 15 plt.axis(‘off‘) 16 plt.subplot(122) 17 plt.imshow(iimg , cmap = ‘gray‘) 18 plt.title(‘iimg‘) 19 plt.axis(‘off‘) 20 plt.show()

OpenCv实现傅里叶变换
函数
cv2.dft() 和 cv2.idft()
返回结果 = cv2.dft( 原始图像, 转换标识 )
原始图像 首先要使用np.float32() 函数将图像转换为np.float32格式
转换标识的值通常为cv2.DFT_COMPLEX_OUTPUT 用来输出一个复数阵列
函数cv2.dft()返回的结果和numpy进行傅里叶变换得到的结果一致 , 但是他返回的值是双通道的
第1通道是结果的实数部分,第2通道是结果的虚数部分
使用函数cv2.dft()之后同样需要函数numpy.fft.fftshift()实现将零频率分量移到频谱中心
之后要将其显示出来还要使用函数cv2.magnitude()计算频谱信息的幅度,函数形式
返回值 = cv2.magnitude(参数一,参数二)
参数一:浮点型x坐标值,也就是实部
参数二:浮点型y坐标值,也就是虚部,和参数一具有相同的位数
返回值为 参数一和参数二的平方和的平方根
得到频谱信息的幅度后,通常还要对幅度值进一步转换,以便将图像显示出来,
即将幅度值映射到灰度值的灰度空间[0,255]内,
即公式 result = 20 * np.log( cv2.magnitude(实部,虚部))
1 import cv2 2 import numpy as np 3 img = cv2.imread("/home/miao/dog.jpg" , 0) 4 dft = cv2.dft( np.float32(img) , flags = cv2.DFT_COMPLEX_OUTPUT) 5 print("dft = \n" ,dft) 6 dftshift = np.fft.fftshift(dft) 7 print("dftshift = \n" , dftshift) 8 result = 20 * np.log(cv2.magnitude(dftshift[:,:,0] , dftshift[:,:,1])) 9 print("result = \n" , result)
dft
[[[ 5442629. 0. ] [ 112638.86 720144.94 ] [ 199291.6 295989.75 ] ... [ -73885.945 -117819.76 ] [ 199291.6 -295989.75 ] [ 112638.86 -720144.94 ]] [[-2031877. 118866.445] [ -290884.75 -240315.62 ] [ -69323.47 -217808.45 ] ... [ -80757.25 -214683.94 ] [ 87689.74 -263512.44 ] [ -298817.5 465312.25 ]] [[ 117940.055 419359.5 ] [ 226322.28 229652.14 ] [ -170327.42 -338387.7 ] ... [ -68762.08 216805.8 ] [ -248173.78 344444.22 ] [ 167779.88 156720.78 ]] ... [[ 203563.9 -291130.38 ] [ 31911.941 267805.7 ] [ 142347.9 116130.445] ... [ -151712.56 -62466.57 ] [ -239283.3 -319897.38 ] [ -128576.625 41041.527]] [[ 117940.06 -419359.53 ] [ 167779.88 -156720.78 ] [ -248173.78 -344444.22 ] ... [ 78999.33 209142.4 ] [ -170327.42 338387.7 ] [ 226322.28 -229652.14 ]] [[-2031877.1 -118866.48 ] [ -298817.5 -465312.25 ] [ 87689.74 263512.44 ] ... [ 158813.72 -68133.9 ] [ -69323.47 217808.45 ] [ -290884.75 240315.62 ]]]
dftshift
[[[-3.05175781e-05 1.81000122e+02] [-2.21242020e+02 4.47310547e+02] [-4.91660858e+02 -3.89533997e+02] ... [-7.22862366e+02 -5.56106812e+02] [ 4.91660858e+02 -3.89533997e+02] [ 2.21242020e+02 4.47310547e+02]] [[-5.04687836e+02 -1.13754280e+02] [ 3.67620728e+02 -5.22734070e+02] [ 2.31780884e+02 3.46142975e+02] ... [-1.25527039e+02 3.59883911e+02] [-2.29090759e+02 1.01479324e+02] [-5.85184814e+02 -2.68481232e+02]] [[ 2.69147797e+02 9.58936920e+01] [-3.20615723e+02 2.28430405e+02] [-3.35807678e+02 -5.58035095e+02] ... [ 4.27737488e+02 -3.72080078e+02] [ 3.80756531e+01 2.09622498e+02] [ 2.67722412e+02 -4.23770844e+02]] ... [[-4.27722015e+02 -1.86195862e+02] [ 4.19498779e+02 2.00292221e+02] [-5.37565613e+01 3.44412720e+02] ... [-3.42792969e+01 7.90777832e+02] [-6.05357666e+02 1.66101379e+01] [-1.82286621e+02 -1.37281662e+02]] [[-2.69147888e+02 9.58937073e+01] [-2.67722412e+02 -4.23770844e+02] [-3.80756531e+01 2.09622498e+02] ... [ 4.04659668e+02 -5.31339905e+02] [ 3.35807678e+02 -5.58035095e+02] [ 3.20615723e+02 2.28430405e+02]] [[ 5.04687744e+02 -1.13754257e+02] [ 5.85184814e+02 -2.68481232e+02] [ 2.29090759e+02 1.01479324e+02] ... [ 4.21408844e+02 3.88300781e+02] [-2.31780884e+02 3.46142975e+02] [-3.67620728e+02 -5.22734070e+02]]]
result 可以看出值的范围在 [0 , 255]
[[103.969955 124.25348 128.82753 ... 136.3133 128.82753 124.25348 ] [124.97435 129.19992 120.64148 ... 118.86374 110.47402 129.34885 ] [113.10027 119.510185 129.57889 ... 126.804504 107.23077 124.342316] ... [122.90482 122.834785 117.077515 ... 133.47913 128.12392 108.60434 ] [113.10028 124.342316 107.23077 ... 130.08235 129.57889 119.510185] [124.97435 129.34885 110.47402 ... 127.018745 120.64148 129.19992 ]]
逆变换
1 import cv2 2 import numpy as np 3 import matplotlib.pyplot as plt 4 img = cv2.imread("/home/miao/dog.jpg" , 0) 5 dft = cv2.dft(np.float32(img) , flags = cv2.DFT_COMPLEX_OUTPUT) 6 dftshift = np.fft.fftshift(dft) 7 ishift = np.fft.ifftshift(dftshift) 8 iimg = cv2.idft(ishift) 9 iimg = cv2.magnitude(iimg[:,:,0] , iimg[:,:,1]) 10 Iimg = 20 * np.log(iimg) 11 plt.subplot(221) 12 plt.imshow(img,cmap = ‘gray‘) 13 plt.title("original") 14 plt.axis("off") 15 16 plt.subplot(222) 17 plt.imshow(iimg,cmap = ‘gray‘) 18 plt.title("imverse") 19 plt.axis("off") 20 21 plt.show()

低通高通滤波示例
高通
通过对傅里叶变换后的频谱图像中间部分即低频分量的值替换为0,就屏蔽了低频,实现高通
低通
与高通相反将傅里叶变换后的中间低频部分之外的高频信号值替换为0,实现了低通
1 import cv2 2 import numpy as np 3 import matplotlib.pyplot as plt 4 img = cv2.imread("/home/miao/dog.jpg" , 0) 5 f = np.fft.fft2(img) 6 fshift = np.fft.fftshift(f) 7 rows , cols = img.shape 8 crow , ccol = int(rows/2) , int(cols/2) 9 # 10 mask = np.zeros((rows , cols ) , np.uint8) 11 mask[crow-30:crow+30 , ccol-30:ccol+30] = 1 12 l_shift = fshift.copy() 13 h_shift = fshift.copy() 14 l_shift[crow-30:crow+30 , ccol-30:ccol+30] = 0 15 h_shift = fshift * mask 16 # 17 l_ishift = np.fft.ifftshift(l_shift) 18 h_ishift = np.fft.ifftshift(h_shift) 19 ishift = np.fft.ifftshift(fshift) 20 # 21 iimg = np.fft.ifft2(ishift) 22 l_img = np.fft.ifft2(l_shift) 23 h_img = np.fft.ifft2(h_shift) 24 # 25 iimg = np.abs(iimg) 26 l_img = np.abs(l_img) 27 h_img = np.abs(h_img) 28 # 29 plt.subplot(221) , plt.imshow(img , cmap = ‘gray‘) 30 plt.title(‘original‘) , plt.axis(‘off‘) 31 # 32 plt.subplot(222) , plt.imshow(l_img , cmap = ‘gray‘) 33 plt.title(‘l_img‘) , plt.axis(‘off‘) 34 # 35 plt.subplot(223) , plt.imshow(h_img , cmap = ‘gray‘) 36 plt.title(‘h_img‘) , plt.axis(‘off‘) 37 # 38 plt.subplot(224) , plt.imshow(iimg , cmap = ‘gray‘) 39 plt.title(‘iimg‘) , plt.axis(‘off‘) 40 plt.show()
12,13行复制图像时需要进行深复制,

原文:https://www.cnblogs.com/miaorn/p/12301295.html