一类重要的sheaf是松软层flabby sheaf:
flabby sheaf是局部性质,即只要限制在足够小的邻域上总是flabby的,那么这个层就是flabby的:

关于flabby的两个基本性质:


从five lemma看,前后两个是flabby的则中间的sheaf是flabby的。

flabby resolution的性质是带supports的截断函子可以作用在上面。
而我们总是能对任意sheaf做flabby resolutuon:


而其中用flabby resolution不影响同调的计算。
接下来我们讨论一个section的局部延拓:


现在讨论 faisceaux mous 软层,其弱于松软层,
如果X是仿紧空间,那么利用上述定理,任意集上的flabby sheaf的section都可以先延拓到一个开集上,再延拓到全局上。
以下定理实际上给出了软层的另一定义:

再考虑与support有关的软层:

这里说明的局部有限直和就是给定一族sheaf和一个集合,这个集合上的section仅仅在有限个sheaf中不为0.
以下定理是另外一种定义,实际上说的是,


然后我们考虑和flappy sheaf一个类似的定理,其证明的方法已经出现多次,先在局部上证明是对的,然后用这些局部成立的开集构成一个开覆盖,再用Zorn’s lemma






接着这个partition和一组开覆盖相协调的定义:






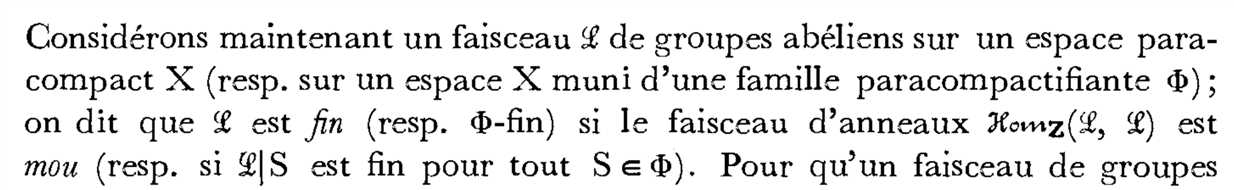
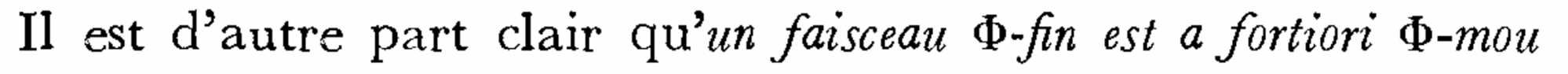

结合张量运算的性质保持:


Godement 《theorie des faisceaux》第三章(上)
原文:https://www.cnblogs.com/zny14/p/12306063.html