一致收敛

一致收敛性是一个在级数、积分运算中经常可以用到的性质，不过高数上并非重点，本文意在整理其定义，以及用通俗的语言描述常用的重要性质，最后一节给出一致收敛函数的判别法。

同时要注意区分数列收敛，函数列一致收敛及内闭一致收敛的区别，这些是初学者容易混淆的概念，应加以注意。

首先声明函数列的定义：

设\(f_1，f_2,\cdots,f_n,\cdots\)是一列定义在同一数据集\(E\)的函数，称为定义在\(E\)上的函数列\(\{f_n\}，（n=1,2,\dots）\),设\(x_0\in E\)，带入函数列可得到数列：
\[ f_1(x_0),f_2(x_0),\cdots,f_n(x_0),\dots\tag{1} \]
若数列（1）收敛，则称函数列在\(x_0\)收敛，若函数列在数集\(D\sub E\)上每一个点都收敛，则称函数列在数集 D 上收敛。即对于\(\forall x\in D\)，存在数列\(\{f_n\}\)的极限值与之相对应，由此映射所对应的 D 上的函数，称为函数列的极限函数，记为：
\[ \lim_{n\to\infty}f_n(x)=f(x)，x\in D\sub E \]

\[ for\ x\in D,\forall\varepsilon>0,\exist N>0,s.t.n>N\ 时\|f_n(x)-f(x)|<\varepsilon \]

函数列的一致收敛性

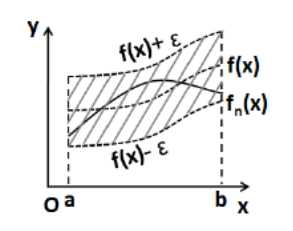
设函数列\(\{f_n\}\)与函数\(f\)定义在同一数集\(D\)上，若对任给的正数\(\varepsilon\)，总存在某一正整数 N ，使得当\(n>N\)时，对一切\(x\in D\),都有：
\[ |f_n(x)-f(x)|<\varepsilon \]
则称函数列\(\{f_n\}\)在 D 上一致收敛于\(f\)，记作：
\[ f_n(x)\rightrightarrows f(x)\quad(n\to\infty)，x\in D \]

一致收敛函数列的性质

• 设函数列\(\{f_n\}\)在\((a,x_0)\bigcup(x_0,b)\)上一致收敛于\(f(x)\)，且对于每一个n，\(f_n(x)\to a_n\quad(x\to x_0)\)，则\(\{a_n\}(n\to\infty)\)和\(f(x)\ (x\to x_0)\)均存在且相等。

一致收敛

原文：https://www.cnblogs.com/rrrrraulista/p/12315242.html