4.Median of Two Sorted Arrays

1.题目描述

英文版：

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

You may assume nums1 and nums2 cannot be both empty.

Example 1:

nums1 = [1, 3]
nums2 = [2]

The median is 2.0
Example 2:

nums1 = [1, 2]
nums2 = [3, 4]

The median is (2 + 3)/2 = 2.5

中文版：

有两个长度分别为m和n的有序数组。

寻找这两个有序数组的中位数，并且保证时间复杂度为O(log (m+n))。

假设这两个数组nums1和nums2都不能为空。

例1：

nums1 = [1, 3]
nums2 = [2]

中位数为 2.0
例2

nums1 = [1, 2]
nums2 = [3, 4]

中位数为 (2 + 3)/2 = 2.5

2.解法

2.1 解法1

思路：

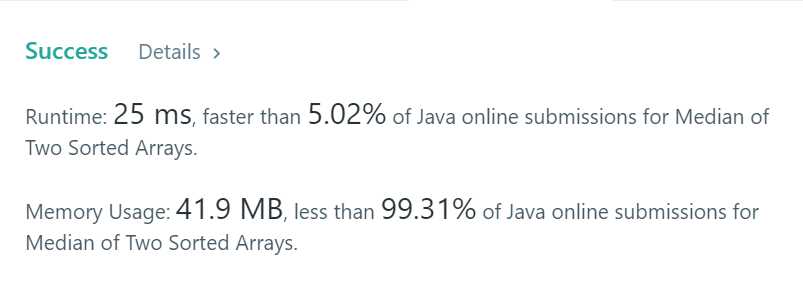
在看完这道题目之后，首先想到的是，将这两个数组合并放到另一个数组中，并进行排序，最后再求中位数。最后发现运行居然需要25秒，时间复杂度非常高。

public static double findMedianSortedArrays1(int[] nums1, int[] nums2) {
        double median;

        int[] nums3 = new int[nums1.length + nums2.length];

        for(int i = 0;i < nums1.length;i++){
            nums3[i] = nums1[i];
        }

        for(int i = 0;i < nums2.length;i++){
            nums3[nums1.length + i] = nums2[i];
        }

        for(int i = 0;i < nums3.length;i++){
            for(int j = i + 1;j < nums3.length;j++){
                if(nums3[i] > nums3[j]){
                    int temp = nums3[i];
                    nums3[i] = nums3[j];
                    nums3[j] = temp;
                }
            }
        }

        if(nums3.length % 2 == 0){
            int index1 = nums3.length / 2;
            int index2 = index1 - 1;
            median = (nums3[index1] + nums3[index2]) / 2.0;
        }else {
            int index = nums3.length / 2;
            median = nums3[index];
        }

        return median;
    }

在LeetCode上运行的结果：

2.2 解法2

思路：

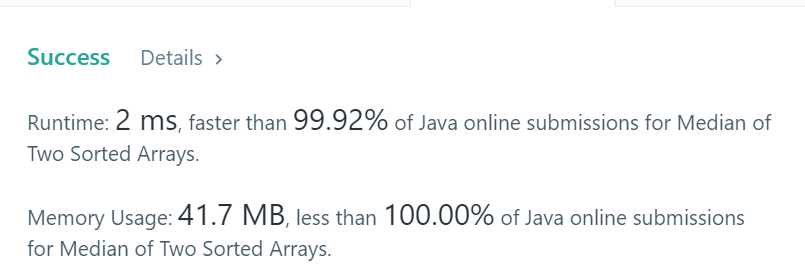
这种做法也是从LeftCode的Solution中得到的，起初看得一脸懵逼，最后看了好多别人写的博客，才把这种思路稍微弄明白。

首先，如果是奇数那么中位数的位置即为(len+1)/2。如果是偶数，那么中位数左边的数的位置也是(len+1)/2。因此，nums1和nums2中位数所在的位置即为half=（alen + blen + 1）/ 2。在Left_A取到的数的个数为apart = (sart+end)/2,Left_B取到的数的个数为bpart = half - apart;最终结果只要符合 aPartLeft < bPartRight 并且 bPartLeft < aPartRight，那么即可找到中位数。如果是奇数那么中位数为 max(aPartLeft,bPartLeft),如果是偶数，那么中位数为（max(aPartLeft,bPartLeft)+min(aPartRight,bPartRight)）/ 2.0

解题思路：

代码实现：

public static double findMedianSortedArrays2(int[] nums1, int[] nums2) {
        int alen = nums1.length;
        int blen = nums2.length;

        if(alen > blen){    //将长度最短的数组放在前面,这样进行二分查找更快
            int[] temp = nums1;
            nums1 = nums2;
            nums2 = temp;

            alen = nums1.length;
            blen = nums2.length;
        }

        int half = (alen + blen + 1) / 2;   //如果两个数组合并且排好迅，中位数的位置。
        boolean even = ((alen + blen) % 2 == 0) ? true:false;

        int start = 0;
        int end = alen;
        int apart = 0;
        int bpart = 0;

        while (start <= end){
            apart = (start + end) / 2;
            bpart = half - apart;
            if(apart > start && nums1[apart-1] > nums2[bpart]){ //left_A不为空，能取到数据 并且 aPartLeft > bPartRight
                end = apart - 1;  //A左移
            }else if(apart < end && nums2[bpart-1] > nums1[apart]){ //right_A不为空，能取到数据 并且 bPartLeft > aPartRight
                start = apart + 1; //A右移
            }else { // 符合 aPartLeft < bPartRight 并且 bPartLeft < aPartRight
                //求leftMax
                int leftMax = 0;
                if(apart == 0){ //left_A为空
                    leftMax = nums2[bpart-1];
                }else if(bpart == 0){ //left_B为空
                    leftMax = nums1[apart-1];
                }else { //常规；left_A和left_B都不为空
                    leftMax = Math.max(nums1[apart-1],nums2[bpart-1]);
                }
                if(!even){ //如果为奇数直接返回leftMax
                    return leftMax;
                }

                //求rightMin
                int rightMin = 0;
                if(apart == alen){ //A所有数小于B的数,right_A为空,则取B数
                    rightMin = nums2[bpart];
                }else if (bpart == blen){ //B所有数小于A的数,right_B为空,则取A数
                    rightMin = nums1[apart];
                }else {//常规，right_A和right_B都不为空
                    rightMin = Math.min(nums1[apart],nums2[bpart]);
                }
                return (leftMax + rightMin) / 2.0;
            }

        }
        return 0.0;
    }

在LeetCode上运行的结果：

3.测试

在本地，我只是简单写了一个main函数来对它进行测试。但是这些代码都是在LeetCode上运行通过了的。

public static void main(String[] args) {
    int[] nums1 = {1, 3};
    int[] nums2 = {2};
    double result = findMedianSortedArrays2(nums1, nums2);
    System.out.println(result);
}

4.Median of Two Sorted Arrays

原文：https://www.cnblogs.com/limaodeng/p/12315607.html