在《机器学习---最小二乘线性回归模型的5个基本假设(Machine Learning Least Squares Linear Regression Assumptions)》一文中阐述了最小二乘线性回归的5个基本假设以及违反这些假设条件会产生的后果。那么,我们怎么检测出是否有违反假设的情况出现以及如何解决出现的问题呢?(注:内生性的问题比较复杂,这里暂时略过。)
非线性的检测
1,残差图(residual plot):x轴是预测值,y轴是残差。用来查看模型是否很好地拟合数据,如果残差分布有规律可循,说明拟合得不好。
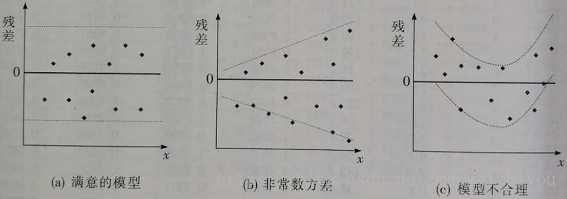
可以看出,上面最后一张图显示可以用非线性模型拟合。(中间这张图是说残差的方差没有保持不变,产生了异方差问题)
2,偏残差图(partial residual plot):用来查看哪个变量需要进行非线性变换。
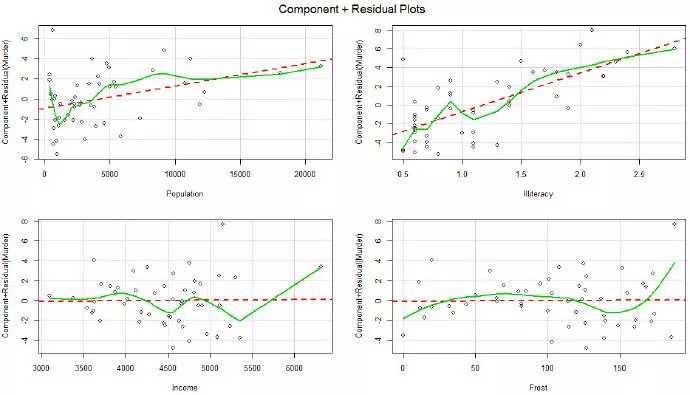
非线性的解决办法
使用特征的非线性变换:https://www.cnblogs.com/HuZihu/p/10144425.html
共线性或多重共线性的检测
1,计算两变量之间的相关关系,如果一组变量之间高度相关,就说明这组变量之间存在共线性问题
2,大部分变量的系数分别不显著(t-test),但是它们又联合显著(F-test),那么就说明它们之间存在多重共线性的问题
3,计算每个变量的方差膨胀因子(variance in?ation factor,VIF):VIF=1/(1−R2),若VIF>10,说明该变量可能存在多重共线性性问题
4,估算出的系数符号与期望相反,比如说变量X1和Y之间应该是正相关关系,结果估算出的该变量的系数β1却是负数,那就说明该变量可能存在多重共线性性问题
共线性或多重共线性的解决办法:
在实际运用中,共线性问题是不可避免的。除了数据本身会带来共线性问题,回归模型的结构也会带来这个问题,比如当有交互项的时候,或用高阶模型的时候。
源于数据的共线性:1,去掉引起共线性的不重要的特征:这点比较难处理,因为你不知道哪个变量是不重要的
2,不做改变(虽然参数不准,但是预测值不受影响):这点不太推荐,因为经常需要向别人解释模型
3,设计一个实验
4,使用加权回归模型
结构化共线性问题: 5,对特征进行标准化处理:https://www.cnblogs.com/HuZihu/p/9761161.html
自相关性的检测:
1,自相关图(Autocorrelation Plot):看是否有截尾或拖尾
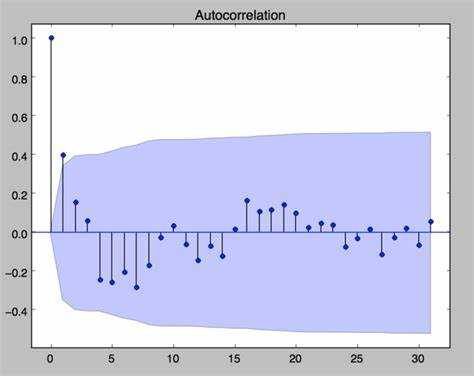
2,残差图:根据时间顺序画出 的残差关系图。
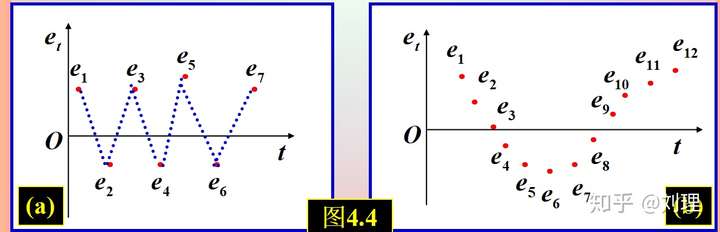
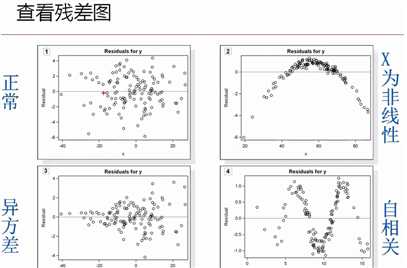
随着时间的推移,如果残差并不是散乱的,而是有序的,这就说明存在自相关性。
3,杜宾-瓦特森检验(Durbin-Watson test)

自相关性的解决办法:
使用时间序列分析
随机误差正态性的检测:
1,Q-Q图:如果图中的散点呈直线状,表示误差为正态分布,否则为非正态分布。
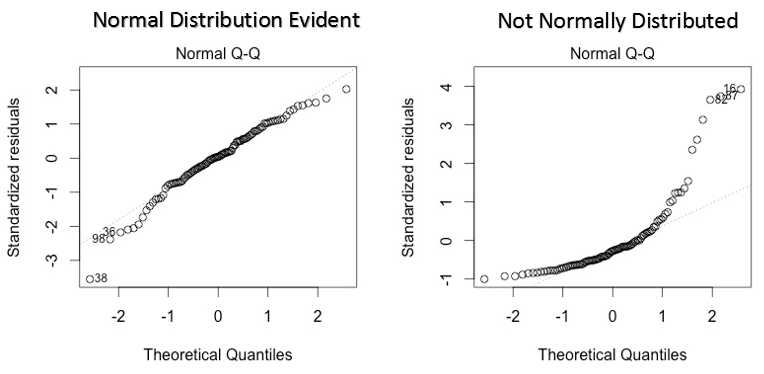
随机误差分布不服从正态分布的解决办法:
对特征进行变换,比如说取对数,平方根等
(注:如果只有轻微偏差,那么不影响模型。)
异方差的检测:
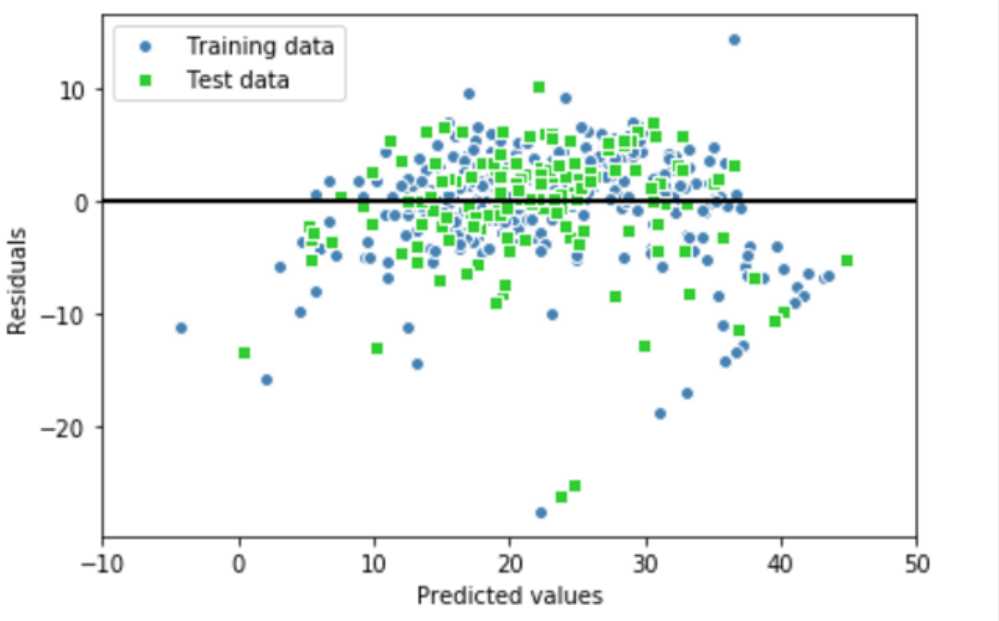
1,残差图:如果异方差存在,会在图中看到明显的规律。
鱼状:
漏斗状:
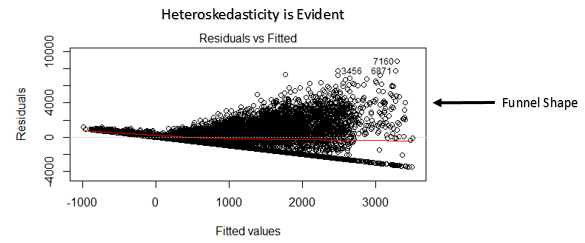
1,漏斗状:对Y进行变换,将Y变为log(Y);鱼状:对Y进行变换,将Y变为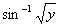
(注:对数变换之后会缩小异方差的范围)
2,改用加权最小二乘法WLS进行估计
(注:加权最小二乘法是对原模型进行加权处理,对较小的残差平方赋予较大的权重,对较大的残差平方赋予较小的权重,这样可以消除其异方差性,然后再使用普通最小二乘法进行参数估计。)
原文:https://www.cnblogs.com/HuZihu/p/12317962.html