python常用排序算法

常见排序算法

• 算法：一个计算过程，解决问题的方法
• 程序 = 数据结构 + 算法

1.算法基本概念

1.时间复杂度

• 用什么方式来体现算法运行的快慢？

  通过运行的次数表示时间复杂度

• 示例：

  print("hello world")
  print("hello python")
  print("hello algorithm")
  #以上时间复杂度O(1)
  
  for i in range(n):
    print("hello world")
    for j in range(n):
        print("hello world")
  #时间复杂度O(n**2)
  
  while n>1:
    print(n)
    n = n//2
  时间复杂度记为O(log 2 n)或O(log n)

  • 当算法过程出现循环折半的时候复杂度式子中会出现log n

• 时间复杂度小结

  时间复杂度是用来计算算法运行的时间的一个式子（单位）
  一般来说，时间复杂度高的算法比复杂度低的算法慢。
  创建的时间复杂度(按效率排序)
    O(1) < O(logn) < O(nlogn) < O(n2) < O(n2 log n) < O(n3)
  复杂问题的时间复杂度
  O(n!)
  O(2**n)
  O(n**n)

• 如何简单快速地判断算法复杂度

  快速判断算法复杂度，适用于绝大多数简单情况
    确定问题规模n
    循环减半过程---> log n
    k层关于n的循环 --->n**k
  复杂情况：根据算法执行判断
  

2.空间复杂度

• 空间复杂度：用来评估算法内存占用大小的式子
• 空间复杂度的表示方式与时间复杂度完全一样
  • 算法使用几个变量：O(1)
  • 算法使用了长度为n的一维列表:O(n)
  • 算法使用了m行n列的二维列表:O(mn)
• 空间换时间

3.递归

• 递归两个条件：
  • 调用自身
  • 结束条件

4.汉诺塔问题

• 把n-1个圆盘从a经过c移动到b
• 把第n个圆盘从a移动到c
• 把n-1个盘子从b经过a移动到c

n = 2 
n = 3 

def hanoi(n,a,b,c):
    """
    n:表示n个盘子
    a:a柱子
    b:b柱子
    c:c柱子
    """
    if n>0:
        hanoi(n-1,a,c,b)#把n-1个盘子从a经过c移动到b
        print('moving from %s to %s'%(a,c))
        hanoi(n-1,b,a,c)#把n-1个盘子从b经过a移动到c

• 汉诺塔移动次数的递推式：h(x) = h(x-1) + 1 + h(x-1)
• h(64) = 18446744073709551615

2.算法8大排序和查找算法

1.顺序查找

• 在一些数据元素中，通过一定的方法找出与给定关键字相同的数据元素的过程
• 列表查找(线性表查找):从列表中查找指定元素
  • 输入：列表，待查找元素
  • 输出：元素下标(未找到元素时一般返回None或-1)

• 内置列表查找函数:index()

• 顺序查找：也叫线性查找，从列表第一个元素开始，顺序进行搜索，直到找到元素或搜索到列表最后一个元素为止

  def linear_search(li,val):
    for ind,v in enumerate(li):
        if v == val:
            return ind
    else:
        return None
  #时间复杂度：O(n)

2.二分查找

• 二分查找：又叫折半查找，从有序列表的初始候选区li[0:n]开始，通过对待查找的值与后选区中间值比较可以使候选区减少一半。（前置条件排序）
• 有序用二分查找，无序先排序再二分查找，时间复杂度会大于顺序查找，如果以后会经常查找，可以进行排序，这样以后查找省事。

from cal_time import *

#计算函数执行时间模块
@cal_time
def binary_search(li,val):
    """
    li:列表
    val:为查找值
    """
    left = 0#列表初值位置
    right = len(li) - 1#列表终止位置
    while left <= right:#候选区有值
        mid = (left + right)//2
        if li[mid] == val:#找到值了，返回索引
            return mid
        elif li[mid] > val:#待查找的值再mid左侧
            right = mid -1
        else:#待查找的值再mid右侧  li[mid] < val
            left = mid + 1
    else:#没有找到
        return None
li = [1,2,3,4,5,6,7,8]
binary_search(li,3)

#时间复杂度：
    #循环折半的时候复杂度式子中会出现log n

3.排序

1.列表排序

• 排序：将一组"无序"的记录序列调整为"有序"的记录序号
• 列表排序：将无序的列表变为有序列表
  • 输入：列表
  • 输出：有序列表
• 升序与降序

• 内置排序函数:sort()

• 常见排序算法

  冒泡排序
  选择排序
  插入排序
  
  快速排序
  堆排序
  归并排序
  
  希尔排序
  计数排序
  基数排序

2.冒泡排序(Bubble Sort)

• 列表每两个相邻的数，如果前面比后面大，则交换这两个数
• 一趟排序完成后，则无序区减少一个数，有序区增加一个数
• 代码关键点:趟/无序区范围。
• 时间复杂度:O(n**2)

def bubble_sort(li):
    for i in range(len(li)-1):#第i趟
        for j in range(len(i)-i-1):
            if li[j] > li[j+1]:
                li[j],li[j+1] = li[j+1],li[j]
        print(li)
li = [1,5,2,3,6]
bubble_sort(li)

• 冒泡排序升级：
  • 如果在一趟过程中，没有发生交换，可以认为就是已经排好序了，后面不用再排了

def bubble_sort(li):
    for i in range(len(li)-1):#第i趟
        exchange = False
        for j in range(len(i)-i-1):
            if li[j] > li[j+1]:
                li[j],li[j+1] = li[j+1],li[j]
                exchange = True
        print(li)
        if not exchange:
            return

3.选择排序(select sort)

• 一趟排序记录最小的数，放到第一个位置
• 再一趟排序记录记录列表无序区最小的数，放到第二个位置
• 不建议选择排序
• 算法关键点：有序区和无序区，无序区最小的数的位置

def select_sort_simple(li):
    new_li = []
    for i in range(len(li)):
        min_val = min(li)
        li_new.append(min_val)
        li.remove(min_val)
    return li_new
li = [3,2,5,10,9,2]
print(select_sort_simple(li))
#不建议写此方法，因为创建了一个列表
#min方法复杂度是O(n),remove方法复杂度是O(n)

• 比较好的选择排序 (原地排序)

def select_sort(li):
    for i in range(len(li)-1):#i是第几趟
        min_location = i
        for j in range(i+1,len(li)):
            if li[j] < li[min_location]:
                min_location = j
        li[i],li[min_location] = li[min_location],li[i]
        print(li)
li = [3,2,5,10,9,2]
select_sort(li)
时间复杂度:O(n**2)

4.插入排序

• 初始时手里(有序区)只有一张牌
• 每次(从无序区)摸一张牌，插入到手里已有的牌的正确位置

def insert_sort(li):
    for i in range(1,len(li)): #i 表示摸到的牌的下标
        temp = li[i]
        j = i - 1#j指的是手里的牌的下标
        while j>=0 and li[j] > temp:
            li[j+1] = li[j]
            j -= 1
        li[j+1] = temp
li = [3,2,5,10,9,2]
print(insert_sort(li))
#时间复杂度：O(n**2)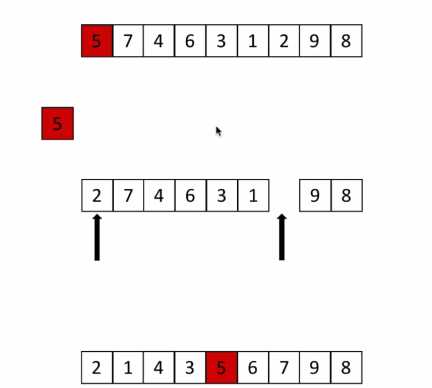

4.快速排序

• 快速排序思路：
  • 取一个元素p,使元素p归位置，列表被p分成两部分，左边都比p小，右边都比p大，循环递归完成。

def partition(li,left,right):
    temp = li[left] #取出一个值
    while left<right:
        while left <right and li[right] >=temp:#从右面找比temp小的数
            right-=1#往左走一步
        li[left] = li[right]#把右边的值写到左边空位
        print(li)
        while left <right and li[left] <= temp:#从左面找比temp大的数
            left += 1
        li[right] = li[left]
    li[left] = temp#把取出的值归位
    return left
#partition函数：取出第一个数temp，让小于temp的数都放在temp左边，大于temp数放在temp右边。

def quick_sort(li,left,right):
    if left<right:#至少2个元素
        mid = partition(li,left,right)
        quick_sort(li,left,mid-1)
        quick_sort(li,mid+1,right)


li = [5,7,4,6,3,1,2,9,9]
quick_sort(li,0,len(li)-1)
print(li)

python常用排序算法

原文：https://www.cnblogs.com/xujunkai/p/12318952.html