0-1背包问题

时间：2020-02-18 00:10:21 阅读：65 评论：0 收藏：0 [点我收藏+]

问题描述：

有 n 件物品和一个最大承重为 W 的背包，每件物品的重量是 ??i、价值是 ??i

在保证总重量不超过 W 的前提下，选择某些物品装入背包，背包的最大总价值是多少？

注意：每个物品只有 1 件，也就是每个物品只能选择 0 件或者 1 件

问题分析：

这是一个典型的动态规划问题：

? 1.设置一个values的物品价值数组和一个相对应的物品重量数组weigths.

? 2.物品的编号为i，由于后续使用数组下标的原因，i从1开始，所以：价值是values[i-1],重量为weights[i-1]。

? 3.状态方程：

dp[i][j] = 表示有前i个物品可以选择，且背包容量为j的情况下可以获取的最大价值

? 4.当 j < weights[ i -1 ]时：

dp[i][j] = dp[i-1][j];

? 5.当 j > = weights[i-1] 时：

dp [i][j] = Math.max (dp[i – 1, j], dp[i – 1, j – weights[i – 1]] + values[i – 1] )
values[i – 1] //表示当前物品的价值  
dp[i – 1, j – weights[i – 1]] // 表示取了当前物品后剩余空间的最大价值
//综合：当j > = weights[i-1] 时，当前的物品可以选择取或者不取
    (1)不取的话，很明显，最大价值就是上一步的最大价值dp[i][j] = dp[i-1][j]
    (2)取的话，价值就为dp[i – 1, j – weights[i – 1]] + values[i – 1]
//由于不知道取还是不取时获得的价值最高，所以对两个数取最大值。

代码实现：

class Solution{
    public void knapsackProblem(){
        int[] weight = {2,2,6,5,4};
        int[] values = {6,3,5,4,6};
        int capacity = 10;
        int n = values.length;
        //因为要空出第一行和第一列 所以dp数组要加一
        int[][] dp = new int[values.length+1][capacity+1];

        for (int i = 1; i < dp.length; i++) {
            for (int j = 1; j < dp[0].length; j++) {
                if (j < weight[i-1]){
                    dp[i][j] = dp[i-1][j];
                }else {
                    dp[i][j] = Math.max(dp[i-1][j],values[i-1]+dp[i-1][j-weight[i-1]]);
                }
            }
        }
      //输出二维数组
        for (int i = 0; i < dp.length; i++) {
            for (int j = 0; j < dp[0].length; j++) {
                System.out.print(dp[i][j] + "  ");
            }
            System.out.println();
        }
      //最终结果
        System.out.println(dp[values.length][capacity]);
    }
}

方案优化

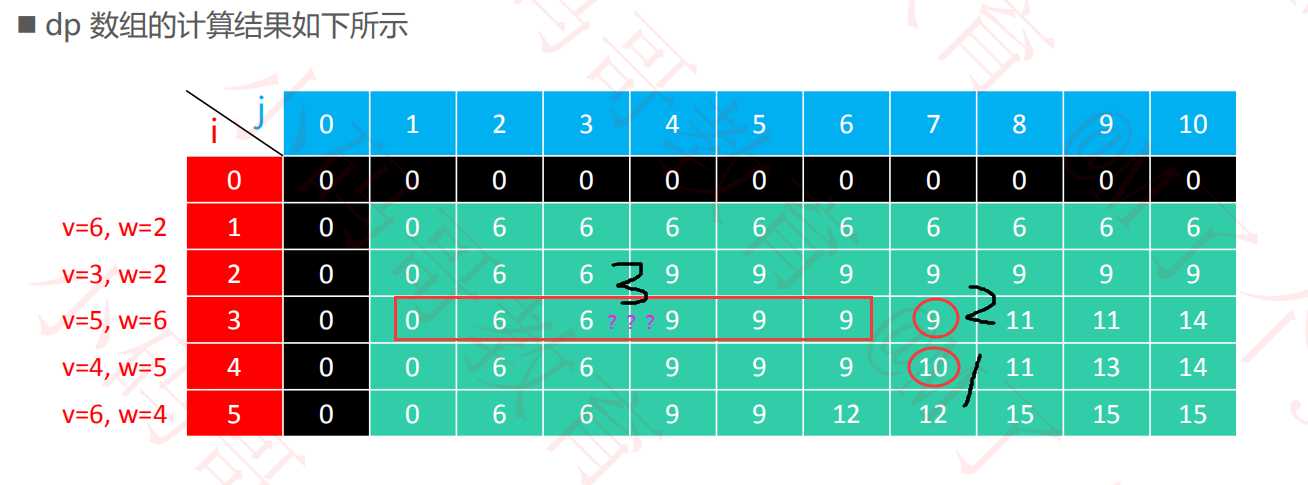
? 比如当我们求dp[4][7]的时候，只有两种选择，要么去4号物品，要么不取。如果不取的话，那这一决策的最大价值就是上一步决策得到的最大价值dp[3][7],如果取的话，就是当前物品的价值加上剩余空间的最大价值dp[ 3 ][ 2 ] = 6, 6+4 = 10.和图中结果一样。

由上一个方案的执行过程我们可以发现这样的规律：

? 当我们求dp[i][j]时，只会用到其当前物品的价值和上一步决策的最大值（2号区域）以及前面的某一个数值（3号区域），那么我们就可以把它简化成一维数组，从后往前求取，这样可以使得代码更加简单。

优化代码实现：

package DynamicProgramming;

public class KnapsackBest {
    public static void main(String[] args){
        int[] w = {1,3,5,4,3};
        int[] v = {5,7,10,8,6};
        int c = 10;
        System.out.println(maxValue(w,v,c));

    }

    public static int maxValue(int[] w,int[] v,int c){
        //判断数组是否符合要求
        if (w.length == 0 || w == null) return 0;
        if (v.length == 0 || v == null) return 0;
        if (w.length != v.length || c <= 0) return 0;
      //用于存储决策价值的数组
        int[] dp = new int[c+1];
        for (int i = 1; i < v.length+1 ; i++) {
            //从后往前遍历，当j < w[i-1]的情况下，直接使用上一步的数组结果
            for (int j = c; j >= w[i-1] ; j--) {
                //从后往前，覆盖上一物品时产生的结果
                dp[j] = Math.max(dp[j],v[i-1] + dp[j-w[i-1]]);
            }
        }

        return dp[c];
    }
}