机器学习-梯度下降基本算法

梯度下降

1.随机梯度下降

 2.使用动量的随机梯度下降

 虽然随机梯度下降仍然是非常受欢迎的优化方法，但学习速率有时会很慢。 动
量方法 (Polyak, 1964) 旨在加速学习，特别是处理高曲率，小但一致的梯度，或是
带噪扰的梯度。 动量算法积累了之前梯度指数级衰减的移动平均，并且继续沿该方
向移动。 动量的效果如图：

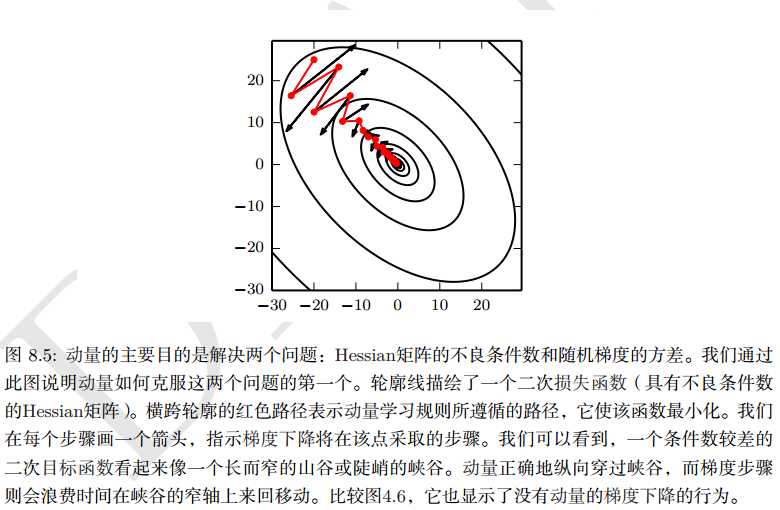
3.AdaGrad

在凸优化背景中， AdaGrad 算法具有一些令人满意的理论性质。然而，经验上
已经发现，对于训练深度神经网络模型而言， 从训练开始时积累梯度平方会导致有
效学习速率过早和过量的减小。 AdaGrad 在某些深度学习模型上效果不错，但不是
全部。
 

4.RMSprop（Root Mean Square Prop）

 修改AdaGrad在非凸情况下更好，改变梯度积累为指数加权的移动平均。Ada算法根据整个历史收缩学习率，可能使得学习率在达到凸结构之前就太小了。

RMS算法使用指数衰减平均以丢弃遥远过去的历史，能够在达到凸碗状结构后快速收敛。

在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度。

5.Adam算法

在Adam 中，动量直接并入了梯度一阶矩（带指数加权）的估计。将动量加入 RMSProp
最直观的方法是应用动量于缩放后的梯度。结合重放缩的动量使用没有明确的理论
动机。其次， Adam 包括负责原点初始化的一阶矩（动量项）和（非中心的）二阶矩
的估计修正偏置（算法8.7）。 RMSProp 也采用了（非中心的）二阶矩估计，然而缺
失了修正因子。因此，不像 Adam， RMSProp 二阶矩估计可能在训练初期有很高的
偏置。 Adam 通常被认为对超参数的选择相当鲁棒，尽管学习速率有时需要从建议
的默认修改。

机器学习-梯度下降基本算法

原文：https://www.cnblogs.com/haimingv/p/12327140.html